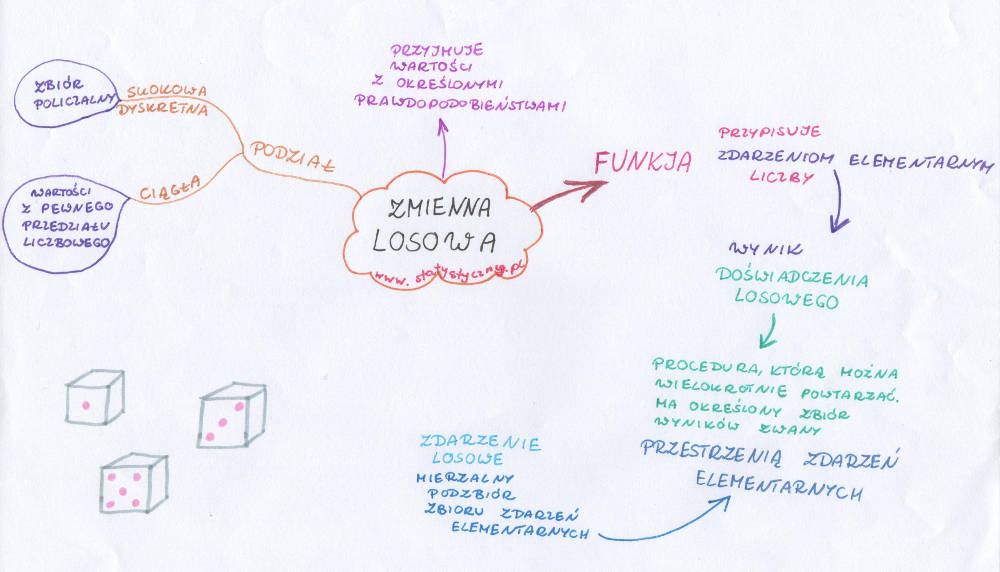
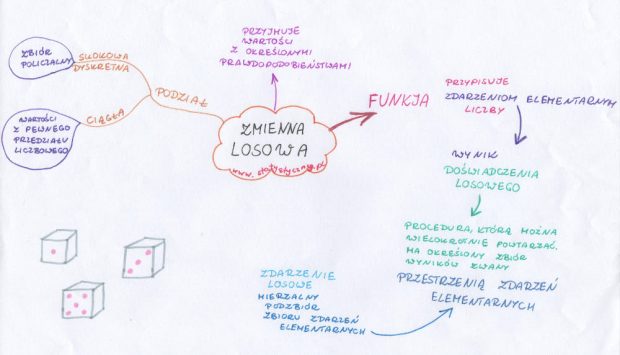
Nigdy nie lubiłam skomplikowanych pojęć statystycznych. Zmienna losowa, jakieś dziwne przestrzenie, zdarzenia elementarne. Nie mogłam pojąć, co to jest i jak się w ogóle zabrać za zrozumienie tych podstaw rachunku prawdopodobieństwa i statystyki. Dzisiaj postanowiłam zmierzyć się z tym tematem po raz kolejny i spróbować przedstawić go w taki sposób, żebyśmy wszystko dobrze zrozumieli.
Zmienna losowa jako funkcja
Zmienna losowa to funkcja. W związku z tym przypomnijmy sobie najpierw, co to jest funkcja. Definicja jest krótka i pewnie wielu z Was (podobnie jak i ja) musiało wbić ją sobie do głowy na którymś z etapów edukacji. Funkcja to takie przyporządkowanie, które każdemu elementowi ze zbioru X przyporządkowuje dokładnie jeden element ze zbioru Y. I to już koniec definicji. Warto zwrócić uwagę na słowa „każdemu elementowi ” i „dokładnie jeden element”. Z definicji wynika, że mamy dwa zbiory. Pierwszy z nich jest nazywany zbiorem X. I każdemu z jego elementów musimy przypisać jakąś inną wartość (ze zbioru Y). Nie możemy pominąć żadnego z elementów. Każdy element z X musi mieć przypisaną jakąś wartość ze zbioru Y. I co więcej – dokładnie jedną wartość z tego zbioru Y. Dla takiego samego x, y zawsze musi przyjąć taką samą wartość.
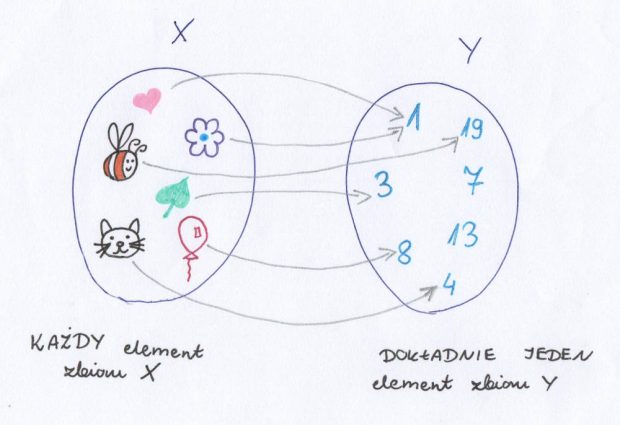
Spójrzmy na powyższy przykład.
W zbiorze X mamy 6 elementów: serduszko, kwiat, pszczołę, listek, kota i balon. W zbiorze Y mamy 7 elementów. Są to liczby 1, 3, 4, 7, 8, 13 i 19. Nasza narysowana funkcja przypisuje każdemu elementowi ze zbioru X dokładnie jeden element ze zbioru Y. Serduszko ma przypisaną jedynkę, pszczoła – dziewietnastę, listek – trójkę itd. Warto zwrócić uwagę, że w zbiorze X nie ma żadnego elementu, który by nie był przypisany do jakiegoś elementu z Y. Natomiast odwrotnie to nie działa – w zbiorze Y moga pozostać elementy bez przyporządkowania (w naszym przypadku są to 7 i 13). Może też się zdarzyć, że różne elementy ze zbioru X będą mieć przypisane ten sam element ze zbioru Y (w naszym przypadku serce i kwiatek mają przypisane ten sam element – jedynkę ze zbioru Y).
OK, zróbmy krok dalej. Zmienna losowa to funkcja, która przypisuje zdarzeniom elementarnym liczby. Co to jest liczba, to raczej wszyscy wiemy. I różne liczby będą stanowić nasz zbiór Y. Sprawdźmy natomiast, co to jest zdarzenie elementarne.
Zdarzenie elementarne oraz jego przestrzeń
Zdarzenie elementarne to wynik doświadczenia losowego.
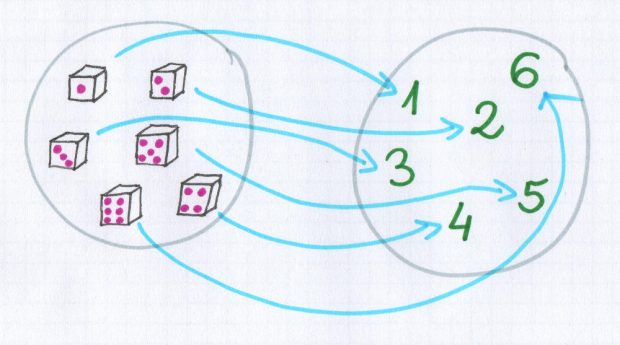
I znów pojawia się pytanie, czym w takim razie jest doświadczenie losowe. Można powiedzieć, że doświadczenie losowe, to każda czynność, która może zakończyć się różnymi nieprzewidywalnymi wynikami. Np. rzut tradycyjną sześcienną kostką do gry. Rzucamy kostką i wychodzi nam pięć oczek. Te pięć oczek to właśnie wynik doświadczenia losowego, czyli nasze zdarzenie elementarne. Inaczej mówiąc, doświadczenie losowe, to procedura, którą można powtarzać wiele razy i ma określony zbiór wyników zwany przestrzenią zdarzeń elementarnych. W wyniku rzutu kostką mamy przestrzeń zdarzeń elementarnych, która składa się z wyników jedno oczko, dwa oczka, trzy oczka, cztery oczka, pięć oczek oraz sześć oczek.
Oto obrazek dla naszych rzutów kostką:
Przykłady zdarzeń losowych
I jeszcze możemy sobie dodać definicję zdarzenia losowego – jest to mierzalny podzbiór zbioru zdarzeń elementarnych.
Kilka przykładów:
A = {6} – wypadło 6 oczek
B = {1, 2} – wypadły mniej niż 3 oczka
C = {1, 3, 5} – wypadła nieparzysta liczba oczek
O monetach słów kilka
Innym tradycyjnym przykładem w rachunku prawdopodobieństwa jest rzut monetą. Tu też mamy zbiór zdarzeń elementarnych Ω={orzeł, reszka}. Jeśli chodzi o zmienną losową to musimy naszym zdarzeniom elementarnym przypisać liczby. Np. orzeł = 0, reszka = 1. I możemy podać sobie przykład zdarzenia losowego A = {0} – rzuciliśmy monetą i wypadł nam orzeł.
Na zakończenie przepraszam wszystkich znawców tematu za wszelkie uproszczenia. Mam jednak nadzieję, że dzięki tym uproszczeniom zmienna losowa przestanie być koszmarem początkujących statystyków.
Tradycyjnie zapraszam do polubienia strony na Facebooku albo do innej próby zaprzyjaźnienia się z blogiem statystycznym.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska