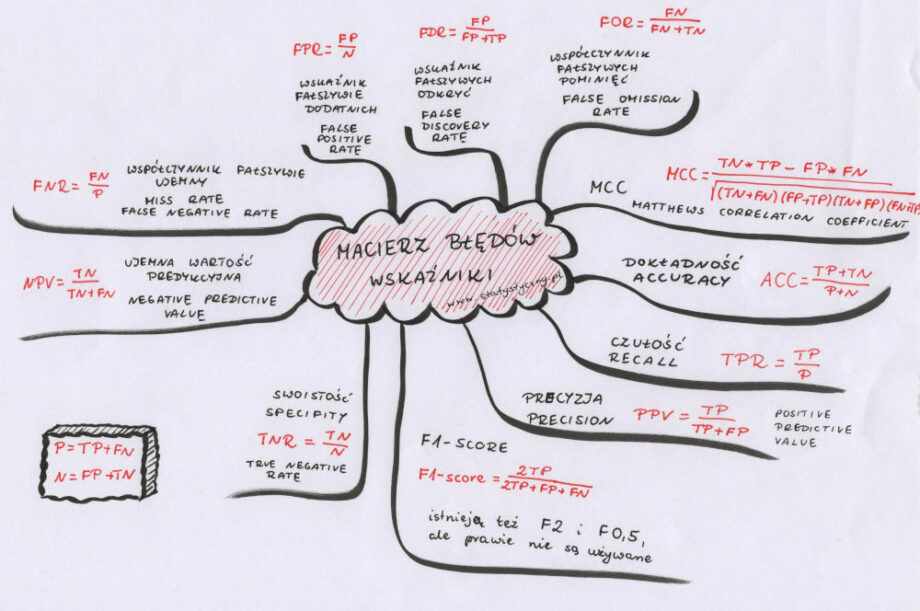
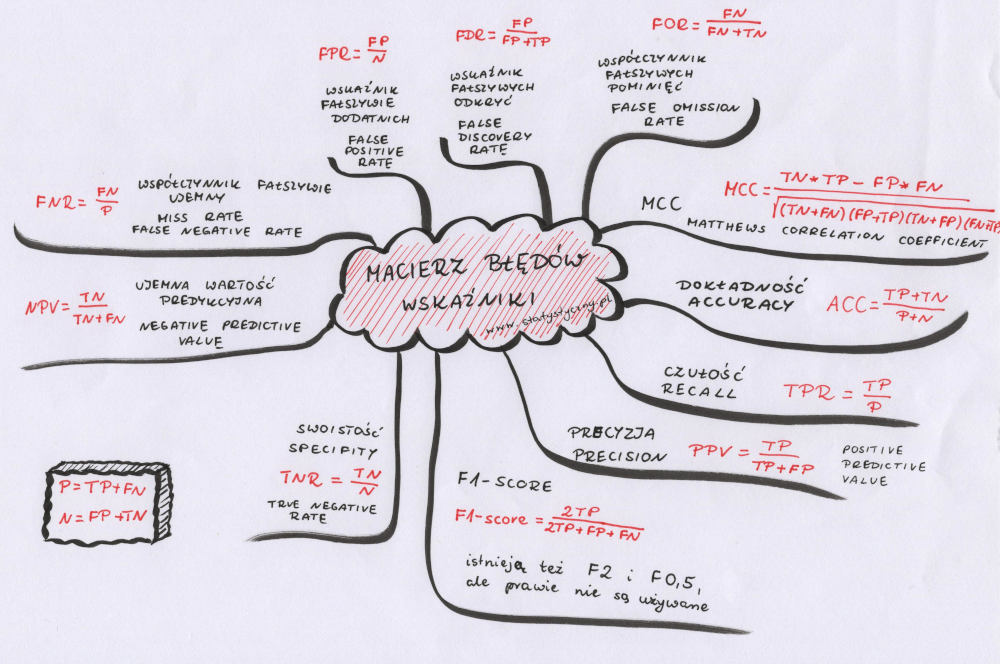
No dobrze, klasyfikuję tekst za pomocą metod machine learning. Ale raz to działa, a raz nie działa. Pojawiają się błędy. Jak sprawdzić, czy te błędy są duże? Które kategorie są najczęściej niedoszacowane? A do których trafiają najczęściej nasze teksty? Jaka jest dokładność naszej klasyfikacji?
Z jak najdokładniejszą analizą jakości naszej klasyfikacji pomoże nam macierz błędów (inaczej zwana tablicą pomyłek, a po angielsku confusion matrix).
Macierz błędów – prognoza versus rzeczywistość
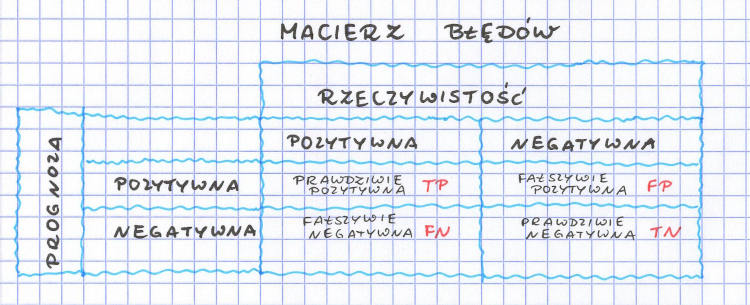
Rysunek macierzy błędów już mamy. Myślę, że powinien Wam się kojarzyć z tabelką błędów, którą prezentowałam w arykule o hipotezach statystycznych. Ale dokładnie co tu mamy? Kiedy przygotowujemy nasz algorytm klasyfikujący, to mamy grupę uczącą, walidacyjną i testową. I kiedy już nauczymy i odpowiednio dobierzemy hiperparametry, to chcemy przetestować, na ile dobrze sprawdza się nasz algorytm dla danych, których nigdy wcześniej nie widział. Bierzemy więc naszą grupę testową i prognozujemy kategorię dla każdego tekstu (prognoza). Przy czym, ponieważ mamy do czynienia z nauczaniem nadzorowanym (było już o tym w pierwszym artykule na temat machine learning), to wiemy, w jakiej kategorii każdy tekst powinien się znaleźć (rzeczywistość).
I teraz robimy macierz błędów dla każdej z kategorii. Jeśli dany tekst trafił prawidłowo do swojej kategorii (np. wyczekiwany mail, nie-spam do skrzynki odbiorczej), to mamy do czynienia z klasyfikacją prawdziwie pozytywną (ang. True Positive) oznaczaną jako TP. Jeśli tekst z innej kategorii trafił prawidłowo do swojej kategorii (np. spam do spamu) to mamy prawdziwie negatywne dopasowanie (ang. True Negative) – TN. Jeśli tekst z naszej kategorii trafił nieprawidłowo do innej kategorii (np. nie-spam do spamu) to mamy do czynienia z fałszywie negatywną kategoryzacją (ang. False Negative), czyli FN. No i jeszcze może być sytuacja, kiedy tekst z innej kategorii trafia do naszej analizowanej (czyli kiedy to ten spam trafia do naszej skrzynki odbiorczej) i wtedy mamy fałszywie pozytywną predykcję (ang. False Positive) oznaczaną FP.
Te literki TP, TN, FN i FP będą nam się przydawać do obliczenia różnych wskaźników więc warto dobrze zrozumieć, skąd się biorą i kiedy zaklasyfikowany tekst wpada do której kategorii.
Zapamiętajmy jeszcze dwa równania, które również mogą nam się w różnych momentach przydać: TP+FN=P oraz TN+FP=N. Czyli na pozytywną kategorię składają się wszystkie pozytywne przypadki zaklasyfikowane prawidłowo do pozytywnej oraz błędnie do negatywnej. Negatywna kategoria to wszystkie negatywne przypadki, które zostały prawidłowo zaklasyfikowane do kategorii negatywnej oraz błędnie – do kategorii pozytywnej.
macierz błędów – rodem z warzywniaka
Spamy i nie-spamy to taki tradycyjny przykład, ale żeby sobie dobrze wszystko w głowach poukładać, spróbujmy przerobić jeszcze jakiś inny. Dla odmiany taki z warzywniaka. Mamy jabłka i pomidory. Niby zupełnie różne, ale czasem i trochę podobne. Mamy też model, który na zdjęciu próbuje rozpoznać, czy mamy do czynienia z jabłkiem czy pomidorem. Idzie mu to raz lepiej, raz gorzej. Jeśli założymy, że naszym „pozytywnym” przypadkiem jest jabłko, to macierz błędów będzie wyglądać następująco:
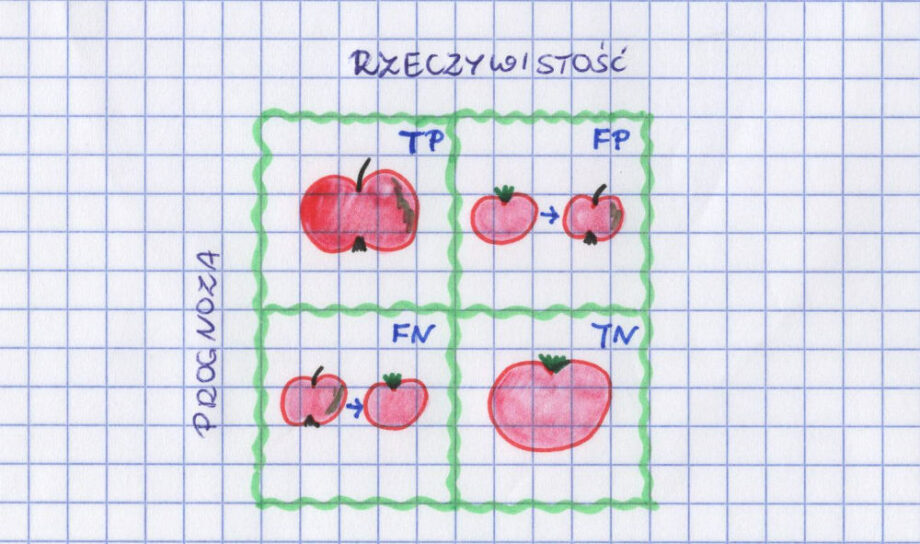
TP to jabłka rozpoznane jako jabłka.
TN to pomidory rozpoznane jako pomidory.
FN to jabłka, które zostały błędnie rozpoznane jako pomidory.
FP to pomidory, które zostały błędnie rozpoznane jako jabłka.
P to wszystkie jabłka – zarówno te rozpoznane prawidłowo, jak i te omyłkowo uznane za pomidory.
N to wszystkie pomidory – pomylone z jabłkami oraz prawidłowo rozpoznane przez algorytm.
raport z klasyfikacji (ang. classification report)
Macierz błędów to pierwszy krok. Kiedy robimy sobie klasyfikację, korzystając z biblioteki scikit learn w Pythonie, możemy poprosić o również wydruk raportu „classification report”. Opiera się on właśnie na wartościach z macierzy błędów, ale o tym wszystkim poniżej.
W tym przykładzie klasyfikujemy różne zdania napisane w 3 językach: po angielsku, po polsku i po hiszpańsku. Zadaniem algorytmu jest prawidłowa klasyfikacja zdania do odpowiedniego języka. W grupie testowej mamy 54 zdania i dla niej budujemy raport z klasyfikacji:
print(classification_report(y_test, y_predicted))
W efekcie dostaniemy taką tabelkę:
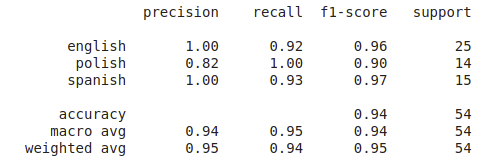
Pojawiają się takie pojęcia jak precision, recall, F1-score, support i accuracy. Zaraz będę je po kolei tłumaczyć. Bo co z tego, że będziemy wiedzieć, ile wynoszą, jeśli nie wiemy, co oznaczają. I czy lepiej, że wynoszą 0.45 czy lepiej, gdyby było to 1.00?
wsparcie (ang. support)
Zaczynam od wsparcia, bo to chyba najłatwiejsza do zrozumienia wartość z raportu klasyfikacji. Mówi o tym, ile przykładów z danej kategorii zostało wylosowanych do grupy testowej. Czyli jeśli klasyfikujemy teksty w różnych językach obcych i do grupy testowej zostały przypisane 54 zdania, to właśnie one pojawią się w pozycji support. A dla każdego języka pojawi się taka liczba, która mówi, ile dokładnie zdań w grupie testowej było napisanych w tym języku. Powyższa tabelka pokazuje, że algorytm był testowany na 25 zdaniach w języku angielskim, 14 zdaniach z języka polskiego i 15 zdaniach napisanych po hiszpańsku.
dokładność (ang. accuracy)
\(ACC=\frac{TP+TN}{P+N}\)Dokładność, to najczęściej podawany wskaźnik, który pozwala nam ocenić jakość klasyfikacji tekstu. Dowiadujemy się, jaka część tekstów, ze wszystkich zaklasyfikowanych, została zaklasyfikowana poprawnie. Czyli sumę poprawnych klasyfikacji z danej kategorii (TP) oraz poprawnej z innych kategorii (TN) dzielimy przez liczbę wszystkich klasyfikowanych przypadków. Jeśli klasyfikowaliśmy wiersze Tuwima oraz wiersze Mickiewicza, to sumujemy poprawnie zaklasyfikowane jedne i drugie i dzielimy przez liczbę analizowanych wierszy. I dokładność powie nam, ile procent z tych wierszy zostało zaklasyfikowanych poprawnie.
I niektórym ta informacja wystarcza.
A dlaczego nie zawsze dokładność dobrze opisuje proces klasyfikacji? Wyobraźmy sobie, że zajmujemy się klasyfikacją, w której chcemy zaklasyfikować maile do spamu i nie do spamu. I załóżmy, że na nasze konto przychodzi bardzo dużo śmieciowych maili, a wśród nich pojedyncze, które są wyjątkowo ważne. Jeśli 95% będą stanowić wiadomości niechciane, a 5% te istotne, to nawet jeśli algorytm wszystko zaklasyfikuje do spamu, to dokładność i tak wyniesie 95%. A nam przecież zależy, żeby jednak odsortować ważne wiadomości i żeby żadna nie zginęła.
Warto równocześnie pamiętać, że im wyższa dokładność tym lepiej. Dokładność 1.00 oznacza, że wszystko jest idealnie dopasowane i algorytm nie pomylił się ani razu.
czułość (ang. recall, sensivity, true positive rate)
\(TPR=\frac{TP}{P}=\frac{TP}{TP+FN}\)Czułość mówi nam o tym, jaki jest udział prawidłowo zaprognozowanych przypadków pozytywnych (TP) wśród wszystkich przypadków pozytywnych (również tych, które błędnie zostały zaklasyfikowane do negatywnych – FN).
Przy czym warto pamiętać, że jeśli algorytm nie zaklasyfikuje żadnego pozytywnego przypadku błędnie (czyli nic nie trafi do kategorii FN), to czułość będzie wynosić 1. Nawet jeśli będzie błędnie klasyfikował FP, czyli negatywne przypadki będą trafiać do kategorii pozytywnej.
Czułość również jest parametrem, który powinien przyjmować jak największą wartość (czyli dążyć do jedynki).
precyzja (ang. precision, positive predictive value)
\(PPV=\frac{TP}{TP+FP}\)Dzielimy liczbę prawidłowo zaprognozowanych pozytywnych wartości (TP) przez sumę wszystkich zaprognozowanych pozytywnie (również tych błędnie zaprognozowanych w ten sposób), czyli TP+FP. W efekcie dowiadujemy się, ile wśród przykładów zaprognozowanych pozytywnie jest rzeczywiście pozytywnych.
Precyzja, podobnie jak dokładność i czułość, powinna przyjmować wartość jak najbliższą 1.00.
F1-score
\(F_1-score=\frac{2TP}{2TP+FP+FN}\)F1-score to średnia harmoniczna pomiędzy precyzją (precision) i czułością (recall). Im bliższa jest jedynki, tym lepiej to świadczy o algorytmie klasyfikującym. W najlepszym przypadku przyjmuje wartość 1, kiedy mamy do czynienia z idealną czułością i precyzją.
Przy czym uwaga, uwaga, bo o tym rzadko się mówi… F1-score to tylko jeden ze wskaźników z całej rodziny F-measures. Używamy go wtedy, kiedy precyzja i czułość są dla nas tak samo ważne. Jeśli nie są, to warto skorzystać z ogólnego wzoru na F-beta score:
\(F_{beta} score=\frac{(1+beta^2)*Precision*Recall}{(beta^2)*Precision+Recall}\)Jeśli beta wynosi 1, to właśnie mamy do czynienia z najbardziej popularnym F1-score, które uwzględnia równie mocno czułość i precyzję. Jeśli precyzja jest dla nas ważniejsza, chcemy minimalizować wartości FP, to korzystamy z F0.5-score. W sytuacji, kiedy chcemy minimalizować wartości FN i ważniejsza jest dla nas czułość od precyzji, to korzystamy z F2-score.
F-score jest często używane podczas oceny algorytmów klasyfikujących dla więcej niż dwóch klas. W jaki sposób je wtedy liczymy? Tę informację znajdziecie pod koniec wpisu.
Podsumowanie: czułość, precyzja, F-score
Jeśli przyjrzymy się dobrze wzorom na czułość i precyzję (i łączący obydwa F-score), to zauważymy, że zupełnie nie przejmują się wartościami TN. Tak więc należy ich unikać, jeśli ta wartość jest dla nas istotna. Jeśli musimy dobrze klasyfikować zarówno przypadki z kategorii „pozytywnej” jak i „negatywnej”, to trzeba poszukać innych wkaźników, które nam w tym pomogą. Na szczęście czułość i precyzja (i powiązane z nimi F-score) to nie wszystko, co możemy „wyciągnąć” z macierzy błędów.
Inne wkaźniki
Powyżej opisałam wszystkie wskaźniki z raportu z klasyfikacji. Mam nadzieję, że już wiecie, o co w nich chodzi. Ale nie są to wszystkie wskaźniki, które możemy wyliczyć na podstawie danych z macierzy błędów. Poniżej przedstawię jeszcze kilka – dużo rzadziej używanych, ale a nuż któryś Wam się przyda.
Swoistość, odsetek prawidziwie negatywnych (ang. specifity, true negative rate)
\(TNR=\frac{TN}{N}\)Swoistość jest tym dla klasy „negatywnej”, czym czułość dla klasy „pozytywnej”. Mierzymy, jak dużo ze wszystkich negatywnych przypadków zostało rzeczywiście zaklasyfikowanych do tej kategorii.
Duża swoistość pokazuje, że klasyfikator rzadko się myli, jeśli chodzi o negatywne przypadki. Tak więc jeśli pokaże, że coś jest pozytywne, to możemy z dużym prawdopodobieństwem się spodziewać, że takie rzeczywiście jest.
Negatywna wartość predykcyjna (ang. negative predictive value)
\(NPV=\frac{TN}{TN+FN}\)Licząc negatywną wartość predykcyjną mierzymy, ile wśród przykładów zaprognozowanych negatywnie jest rzeczywiście negatywnych. Robimy to dzieląc liczbę prawidłowo zaprognozowanych negatywnych wartości (TN) przez sumę wszystkich zaprognozowanych negatywnie (również tych błędnie zaprognozowanych w ten sposób), czyli TN+FN.
Negatywna wartość predykcyjna powinna przyjmować wartości jak najbliższe 1.
Prawidłowy również jest wzór: NPV = 1 – FOR
Współczynnik fałszywie ujemny (ang. miss rate, false negative rate)
\(FNR=\frac{FN}{P}\)FNR to jeden z tych wskaźników, które chcemy, żeby były jak najbliżej 0. Mówi nam o tym, jaki jest stosunek fałszywie negatywnych przypadków do wszystkich przykładów z kategorii pozytywnej. Można go również obliczyć poprzez odjęcie wartości czułości od 1.
FNR = 1 – TPR
Wskaźnik fałszywie dodatnich (ang. fall-out, false positive rate)
\(FPR=\frac{FP}{N}\)FPR również powinien być jak najbliższy 0. Mówi o tym, jaki jest udział fałszywie pozytywnych przypadków wśród wszystkich przypadków z kategorii negatywnej. Suma FPR oraz swoistości (TNR) wynosi 1.
FPR = 1-TNR
Wskaźnik fałszywych odkryć (ang. false discovery rate)
\(FDR=\frac{FP}{FP+TP}\)Wskaźnik fałszywych odkryć obliczamy poprzez podzielenie liczby fałszywie pozytywnych przypadków przez wszystkie przypadki, które zostały zaprognozowane pozytywnie (zarówno prawidłowo TP, jak i nieprawidłowo FP).
FDR = 1 – PPV
Współczynnik fałszywych pominięć (ang. false omission rate)
\(FOR=\frac{FN}{FN+TN}\)Współczynnik fałszywych pominięć mówi nam o tym, ile wśród przykładów zaprognozowanych negatywnie (TN + FN) jest błędnie zaklasyfikowanych jako negatywne (FN). Chcemy, żeby FOR był jak najbliższy 0.
FOR = 1 – NPV
MCC, Współczynnik korelacji Matthews (ang. Matthews Correlation Coefficient)
\(MCC=\frac{TN*TP – FP*FN}{\sqrt{(TN+FN)(FP+TP)(TN+FP)(FN+TP)}}\)Dokładność jest bardzo wrażliwa w przypadku niezrównoważonych klas. Precyzja, czułość, F1-score są niesymetryczne. I jak tu wybrać coś, co w miarę obiektywnie powie nam, czy dobrze udało nam się dokonać klasyfikacji? Tutaj na pomoc przychodzi współczynnik korelacji Matthews.
Jeśli nazwa współczynnik korelacji coś Wam mówi, to bardzo dobrze. W historii bloga znajdziecie dwa artykuły o współczynniku korelacji Pearsona. I MCC ma ze współczynnikiem korelacji Pearsona coś wspólnego. Proponuję, żeby wszyscy zainteresowani potraktowali to jak zagadkę i poszukali, co je łączy.
MCC przyjmuje wartości od -1 do 1 (co nie powinno nas zaskakiwać, bo te same wartości przyjmuje współczynnik korelacji Pearsona). Jeżeli wynosi 1, to znaczy, że nasz model perfekcyjnie klasyfikuje wszystko do prawidłowej kategorii. Jeśli pojawia się zero, to oznacza, że wszystko działa źle i równie dobry (a właściwie równie zły) wynik byśmy mogli otrzymać rzucając monetą albo klasyfikując w inny absolutnie losowy sposób. Wartość -1 oznacza, że wszystko zostało zaliczone do niepoprawnej kategorii.
Warto zwrócić uwagę, że MCC jest symetryczny, co oznacza, że zawsze ma taką samą wartość i nie ma znaczenia, którą klasę uznamy za pozytywną, a którą za negatywną.
Macierz błędów – przykład obliczeń
Jabłka i pomidory w naszym warzywniaku i ich rozpoznawanie na podstawie wyglądu. Może to właśnie dobry przykład, żeby policzyć sobie wszystkie nasze wskaźniki.

Przy czym wydaje mi się, że to jest ten moment, kiedy warto spojrzeć na to wszystko głębiej. Co się stanie jeśli trochę odwrócimy tabelkę i naszą pozytywną klasą będą nie jabłka a pomidory? Nadal będziemy klasyfikować dokładnie to samo. Nadal będziemy mieć dokładnie te same wartości. Tylko zmienimy w naszej macierzy jabłka z pomidorami miejscami.
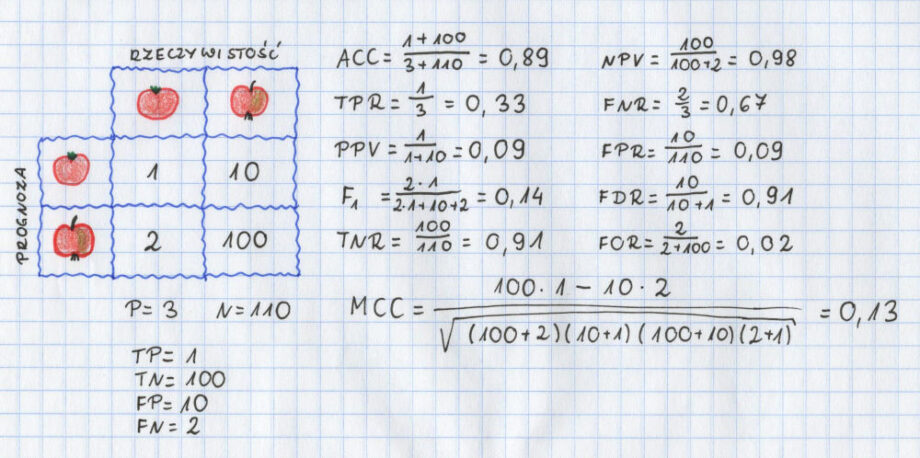
Na co warto zwrócić uwagę? Że wyniki są inne. Oczywiście, nie wszystkie wyniki. Dokładność (accuracy) oraz MCC są dokładnie takie same. Ale pozostałe wyniki już nie. Czułość (TPR) jest inna dla jednego i drugiego. Dla pozytywnych jabłek to 0.91 (czyli całkiem dobry wynik), a dla pozytywnych pomidorów jest to tylko 0.33 (czyli trochę nie najlepiej).
Można jeszcze zauważyć, że TPR i TNR zamienią się miejscami, kiedy zamieniamy kategorie traktowane jako pozytywne. Podobnie jak PPV i NPV oraz FOR i FDR. Wszystko to dlatego, że TP z pierwszego przypadku staje się TN w drugim przypadku. I podobnie FP i FN.
Myślę, że powyższy przykład bardzo dobrze pokazuje, które wskaźniki kiedy powinniśmy liczyć. Pokazuje, że ważny jest wybór klasy uznawanej za pozytywną. Pokazuje, że niektóre wyniki właśnie od tego zależą, a niektóre nie. Jeśli będziecie kiedykolwiek liczyć wskaźniki na podstawie macierzy błędów, to sugeruję zwrócić na to dużą uwagę.
Raport z klasyfikacji raz jeszcze
Jak już omówiliśmy sobie wszystkie wskaźniki, to jeszcze raz wkleję raport z klasyfikacji, który pokazywałam na początku tekstu:

Weźmy pod uwagę, że dla każdej kategorii podawał on osobno wartość precyzji (precision), czułości (recall) oraz F1, jak również wspomniany wcześniej support. Z powyższej analizy na jabłkach i pomidorach, wiemy, że wartości te różnią się w zależności od tego, która kategoria jest uznana za „pozytywną”. I stąd też osobna wartość dla każdego wskaźnika. Jeśli „pozytywny” jest angielski, to mamy precyzję 1, czułość 0.92 oraz f1-score 0.96. Dokładność (accuracy) jest podana tylko raz, bo przecież ta wartość jest niezmienna, niezależnie od tego, którą kategorię traktujemy jako pozytywną.
Macro average versus weighted average
I jeszcze chciałam zwrócić uwagę na fakt, że w powyższych przykładach mamy podaną precyzję, czułość oraz F1-score dla trzech różnych kategorii oraz pod spodem podsumowanie „macro avg” oraz „weighted avg”. W jaki sposób one są liczone?
Macro avg to średnia arytmetyczna z danego wskaźnika dla każdej kategorii. W przypadku precyzji liczymy to następująco:
\(micro-avg-precision=\frac{1.00 + 0.82 + 1.00}{3}=0.94\)Weighted avg to średnia ważona liczbą przypadków z każdej kategorii. W przypadku precyzji byśmy wyliczyli to następująco:
\(weighted-avg-precision=\frac{1.00*25 + 0.82*14 + 1.00*15}{54}=0.95\)W powyższym przykładzie różnice pomiędzy średnią macro a średnią ważoną nie są zbyt duże. Jeśli jednak mamy do czynienia z bardzo niezbalansowanym zbiorem, w którym niektóre kategorie są dopasowane wyraźnie gorzej niż inne, to różnice te mogą być znaczące.
Macierz błędów – z wykorzystaniem biblioteki seaborn
A tak wygląda macierz błędów przygotowana dla powyższego przykładu z wykorzystaniem biblioteki seaborn (Python):
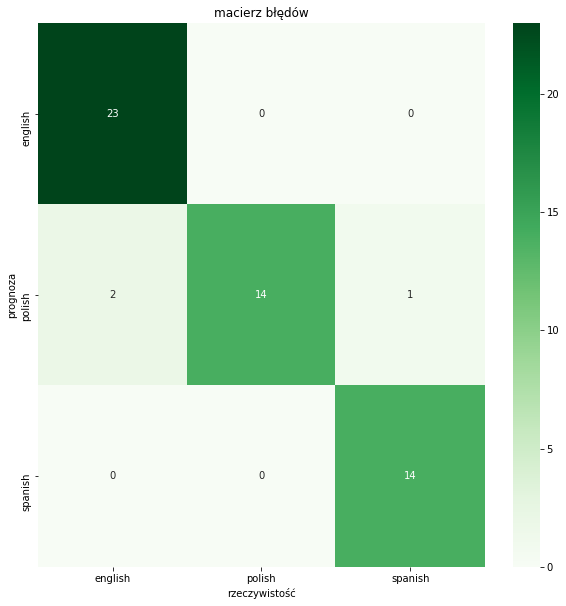
Przy czym uwaga, w powyższej tabeli mamy 3 kategorie, a nie 2. Zinterpretujmy sobie więc prawidłowo nasze TP, TN, FP i FN.
Przyjmijmy za „pozytywną” kategorię język angielski. Mieliśmy 54 zdania, w tym 25 zdań po angielsku. Z tego 23 zdania zostały prawidłowo zaklasyfikowane jako angielskie, 2 błędnie jako polskie. Żadne zdanie z języka polskiego ani hiszpańskiego nie zostało zaklasyfikowane jako angielskie.
TP = 23, TN = 29 (mimo, że jedno z tych 29 nie było zaklasyfikowane prawidłowo, bo było to hiszpańskie zdanie uznane za polskie, ale analizując kategorię angielski – prawidłowo zostało uznane za nie-angielskie), FP = 0, FN = 2. Po podstawieniu do wzorów wszystkie wartości wyjdą nam dokładnie tak samo, jak w raporcie klasyfikacji.
Cieszę się, że mogłam przygotować dla Was kolejny wpis. Mam nadzieję, że dzięki niemu nie będziecie mieć już nigdy więcej problemów z analizą macierzy błędów.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska