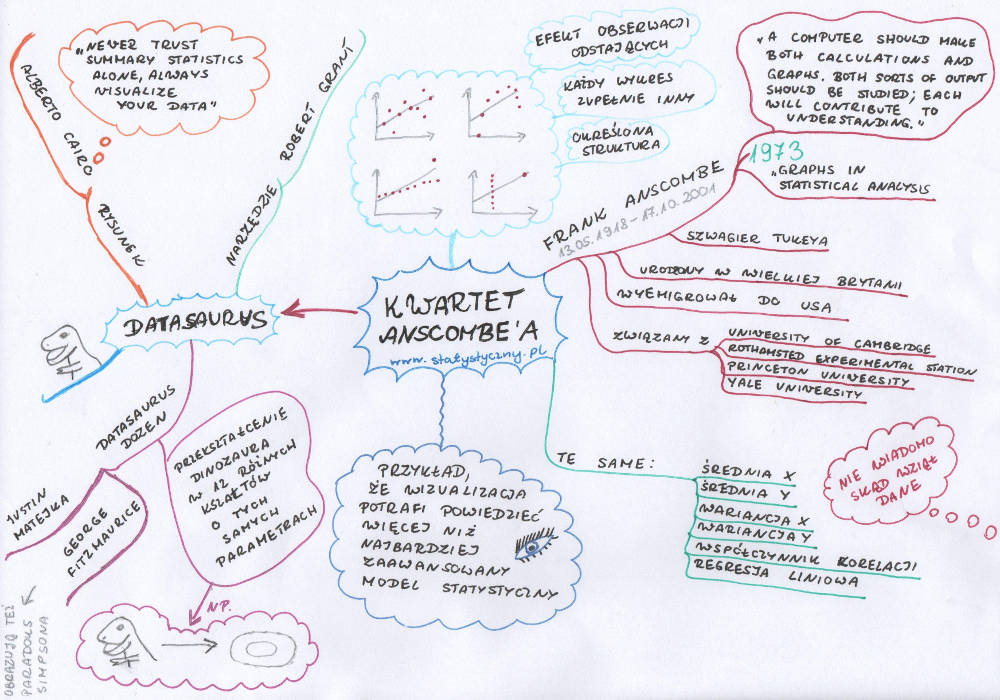
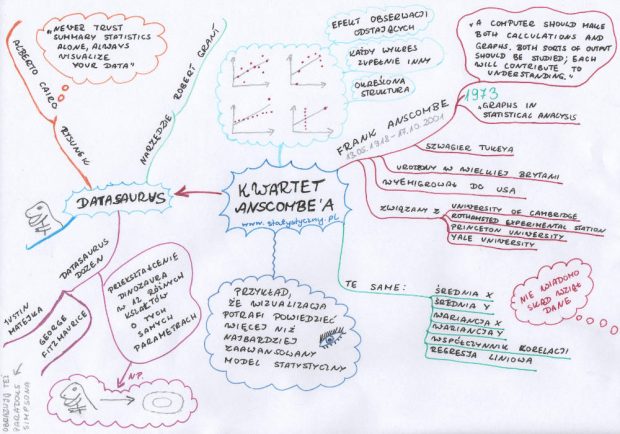
Dawno, dawno temu ludzie nie mieli komputerów. Liczenie było dużo trudniejsze. Potem możliwości zaczęły wzrastać. Nawet duże ilości danych dało się coraz łatwiej przeanalizować i bez wysiłku obliczyć współczynniki korelacji czy parametry regresji liniowej. Graficzne przedstawianie danych stało się coraz mniej modne. Po co rysować, skoro można przeprowadzić skomplikowane obliczenia i podać wzór regresji liniowej? Ale nie wszyscy się zgadzali z takim podejściem do statystyki i właśnie dlatego chciałam przestawić Wam pana Franka Anscombe.
Frank Anscombe to szwagier Johna Tukeya. Pisałam już o Johnie Tukeyu, kiedy wspominałam o wykresie pudełko i wąsy oraz o wykresie łodyga i liście. Jak widać dwie siostry charakteryzowały się podobnym gustem i obie wyszły za mąż za statystyków, którzy lubili rysować. Bo Frank Anscombe też nie uległ modzie na same obliczenia, ale próbował przekonać sobie współczesnych analityków, że rysunki wciąż są potrzebne, żeby jak najlepiej zrozumieć dane statystyczne. W 1973 roku napisał „Graphs in Statistical Analysis”. Niech jedno zdanie z tej pracy będzie naszym dzisiejszym mottem: „A computer should make both calculations and graphs. Both sorts of output should be studied; each will contribute to understanding.” (w moim tłumaczeniu: Komputer powinien robić zarówno obliczenia jak i wykresy. Obydwa wyniki powinny być analizowane, obydwa przyczyniają się do zrozumienia.)
Kwartet Anscombe’a
Tak właściwie to podobno nie wiadomo, skąd Anscombe wziął swoje dane. Ale trzeba przyznać, że przykład robi wrażenie. Mamy 4 zestawy danych dla dwóch zmiennych x i y. W każdym zestawie jest 11 obserwacji.
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 |
| 10.0 | 8.04 | 10.0 | 9.14 | 10.0 | 7.46 | 8.0 | 6.58 |
| 8.0 | 6.95 | 8.0 | 8.14 | 8.0 | 6.77 | 8.0 | 5.76 |
| 13.0 | 7.58 | 13.0 | 8.74 | 13.0 | 12.74 | 8.0 | 7.71 |
| 9.0 | 8.81 | 9.0 | 8.77 | 9.0 | 7.11 | 8.0 | 8.84 |
| 11.0 | 8.33 | 11.0 | 9.26 | 11.0 | 7.81 | 8.0 | 8.47 |
| 14.0 | 9.96 | 14.0 | 8.10 | 14.0 | 8.84 | 8.0 | 7.04 |
| 6.0 | 7.24 | 6.0 | 6.13 | 6.0 | 6.08 | 8.0 | 5.25 |
| 4.0 | 4.26 | 4.0 | 3.10 | 4.0 | 5.39 | 19.0 | 12.50 |
| 12.0 | 10.84 | 12.0 | 9.13 | 12.0 | 8.15 | 8.0 | 5.56 |
| 7.0 | 4.82 | 7.0 | 7.26 | 7.0 | 6.42 | 8.0 | 7.91 |
| 5.0 | 5.68 | 5.0 | 4.74 | 5.0 | 5.73 | 8.0 | 6.89 |
I w każdym przypadku mamy dokładnie takie same wyniki obliczeń:
średnia x wynosi 9
wariancja x wynosi 11
średnia y wynosi 7,50
wariancja y wynosi 4,12
współczynnik korelacji między zmiennymi x i y to 0,816
wzór regresji liniowej wygląda następująco: y = 3 + 0,5x
Wydaje się więc, że wszystkie zestawy danych muszą być podobne, skoro tyle podstawowych statystyk jest identycznych. Wiadomo, jakieś małe różnice są (widać to w danych, że nie są zupełnie takie same), ale nikt nie spodziewa się dużych różnic w sytuacji, kiedy obliczone wyniki są identyczne do kilku miejsc po przecinku. Niespodzianka więc wielka, kiedy patrzymy na wykresy:
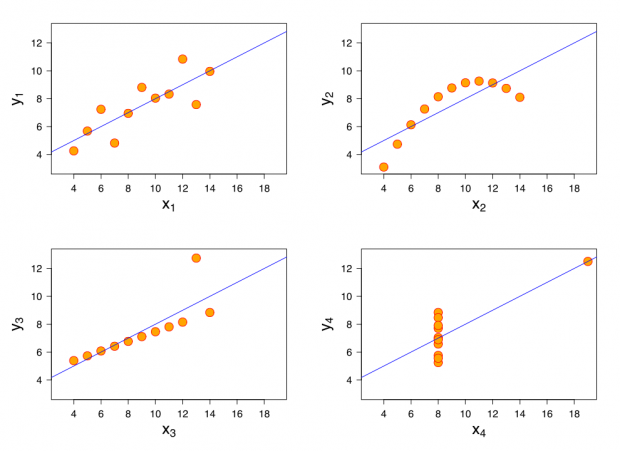
źródło: wikipedia
Kwartet Anscombe’a – nie wszystko jest identyczne
Wiadomo, Anscombe skupił się tylko na miarach klasycznych. Gdyby spojrzał też na miary pozycyjne, to jednak wartości w poszczególnych zestawiach zaczynają się różnić (za wyjątkiem x z pierwszych trzech zestawów, które są po prostu identyczne). Ale jakże często w badaniach skupiamy się tylko na obliczeniu średniej, odchylenia standardowego, współczynnika korelacji i regresji liniowej. Celem Anscombe’a było udowodnienie, że warto skupić się nie tylko na obliczeniach, ale i na rysunku. I cel ten z pewnością udało mu się osiągnąć.
A dla ciekawych przedstawiam poniżej podstawowe miary pozycyjne wyliczone dla danych Anscombe’a za pomocą R:
x1 y1 x2 y2 x3 y3 x4
Min. : 4.0 Min. : 4.260 Min. : 4.0 Min. :3.100 Min. : 4.0 Min. : 5.39 Min. : 8
1st Qu.: 6.5 1st Qu.: 6.315 1st Qu.: 6.5 1st Qu.:6.695 1st Qu.: 6.5 1st Qu.: 6.25 1st Qu.: 8
Median : 9.0 Median : 7.580 Median : 9.0 Median :8.140 Median : 9.0 Median : 7.11 Median : 8
Mean : 9.0 Mean : 7.501 Mean : 9.0 Mean :7.501 Mean : 9.0 Mean : 7.50 Mean : 9
3rd Qu.:11.5 3rd Qu.: 8.570 3rd Qu.:11.5 3rd Qu.:8.950 3rd Qu.:11.5 3rd Qu.: 7.98 3rd Qu.: 8
Max. :14.0 Max. :10.840 Max. :14.0 Max. :9.260 Max. :14.0 Max. :12.74 Max. :19
y4
Min. : 5.250
1st Qu.: 6.170
Median : 7.040
Mean : 7.501
3rd Qu.: 8.190
Max. :12.500
Datasaurus
Kwartet Anscombe’a był motywacją dla kolejnych statystyków, którzy szukali dowodu na to, jak istotne jest rysunkowe przedstawienie danych. Najbardziej fascynujący przykład jaki znalazłam (tak, statystycy potrafią się fascynować wykresami), to Datasaurus.
Wszystko zaczęło się od Roberta Granta. Stworzył niesamowite narzędzie, które pozwala narysować sobie wykres czego tylko się chce. Można następnie zapisać dane i obliczyć wszystkie możliwe parametry.
Narzędzie wykorzystał Alberto Cairo.
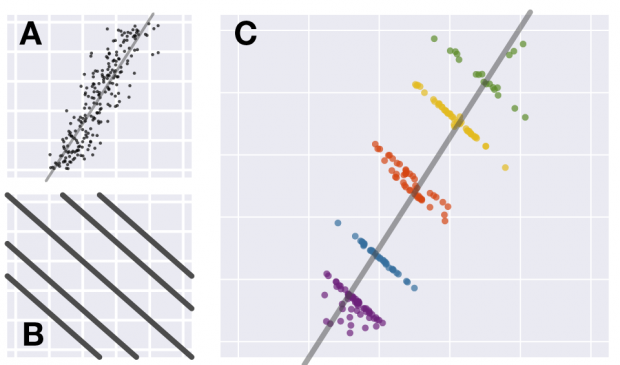
Spójrzcie na te dane:
142 obserwacje. Średnia arytmetyczna x wynosi 54,2633. Ochylenie standardowe x to 16,7651. Średnia arytmetyczna y wynosi 47,8323. Odchylenie standardowe y to 26,9354. Współczynnik korelacji Pearsona pomiędzy zmiennymi x i y równa się -0,0645.
Czy wiecie czego się spodziewać?
Tadam…
Przedstawiam Wam Datasaurusa (ciekawe, czy po polsku powinniśmy go nazywać Danozaurem)… Oto i on we własnej osobie.
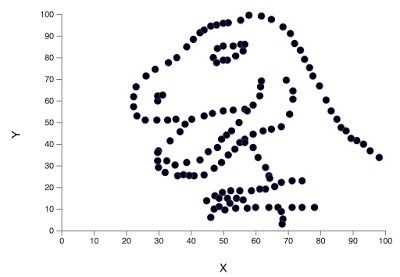
źródło: Alberto Cairo
Datasaurus Dozen
Ale na Alberto Cairo cała zabawa się nie skończyła. Justin Matejka i George Fitzmaurice postanowili pobawić się dalej wizualizacją danych. Wykorzystali Datasaurusa i przekształcili go w 12 różnych innych kształtów – wszystkie o tych samych parametrach statystycznych. To już nie tylko 4 wykresy jak u Anscombe’a. To już cały zestaw. I wszystkie łączy jeden śmieszny dinozaur-danozaur narysowany przez kogoś dla zabawy.
Jeśli tak jak i ja zachwyciliście się pomysłem Datasaurus Dozen, to koniecznie wejdźcie na podlinkowaną stronę i przeczytajcie sobie artykuł, obejrzyjcie animacje. Warto!
A wiecie, co jest w tym wszystkim najciekawsze? Że to dzieje się dzisiaj. Tu i teraz. To nie są prawdy statystyczne sprzed wielu, wielu lat. Alberto Cairo swój twitt z Datasaurusem opublikował w 2016 roku. Artykuł Justina Matejki i George Fitzmaurice’a jest z 2017 roku. I nie wiemy, czy za 200 lat będzie to obowiązkowy element edukacji na studiach statystycznych, czy zostanie zupełnie zapomniany, jak wiele innych odkryć w nauce.
Wizualizacja Paradoksu Simpsona
Nie wiem, czy pamiętacie, ale pisałam już kiedyś o Paradoksie Simpsona. Justin Matejka i George Fitzmaurice zaproponowali w swojej pracy też rysunek, który pomaga zwizualizować sobie tenże paradoks. Myślę, że warto mu się przyjrzeć, żeby lepiej zrozumieć jedną z pułapek statystycznych:
Nawet jeśli tendencja ogólna wydaje się być wzrostowa, to wcale nie znaczy, że dla poszczególnych składników będzie tak samo. Jak w przykładach z poprzedniego wpisu. Być może na całą uczelnię przyjęto mniejszy procent kobiet niż mężczyzn, ale na poszczególnych wydziałach może być zupełnie odwrotnie.
Jak wyrazić swoje uczucia?
I moja własna myśl po zapoznaniu się z tymi ciekawymi grafikami statystycznymi…
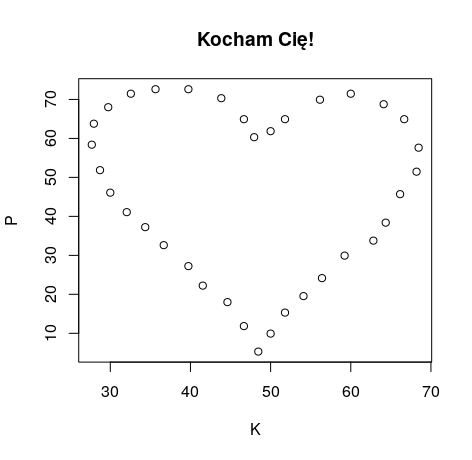
Od teraz, jeśli będziecie chcieli wyrazić swoje uczucia, to zapraszam do korzystania z poniższego zestawu danych (dopasujcie tylko nazwy zmiennych). Myślę, że wybranek/wybranka będą mile zaskoczeni po narysowaniu wykresu:
| K | P |
| 47.9487 | 60.3125 |
| 46.6667 | 64.9279 |
| 43.8462 | 70.3125 |
| 39.7436 | 72.6202 |
| 35.641 | 72.6202 |
| 32.5641 | 71.4663 |
| 29.7436 | 68.0048 |
| 27.9487 | 63.774 |
| 27.6923 | 58.3894 |
| 28.7179 | 51.851 |
| 30 | 46.0817 |
| 32.0513 | 41.0817 |
| 34.359 | 37.2356 |
| 36.6667 | 32.6202 |
| 39.7436 | 27.2356 |
| 41.5385 | 22.2356 |
| 44.6154 | 18.0048 |
| 46.6667 | 11.851 |
| 50 | 61.851 |
| 51.7949 | 64.9279 |
| 56.1538 | 69.9279 |
| 60 | 71.4663 |
| 64.1026 | 68.774 |
| 66.6667 | 64.9279 |
| 68.4615 | 57.6202 |
| 68.2051 | 51.4663 |
| 66.1538 | 45.6971 |
| 64.359 | 38.3894 |
| 62.8205 | 33.774 |
| 59.2308 | 29.9279 |
| 56.4103 | 24.1587 |
| 54.1026 | 19.5433 |
| 51.7949 | 15.3125 |
| 50 | 9.9279 |
| 48.4615 | 5.3125 |
Ja już skorzystałam:
A tymczasem…
Zapraszam do korzystania ze spisu treści i zapoznania się z pozostałymi tekstami na blogu.
Zapraszam na fanpage Statystycznego.
Zapraszam do polubienia i podzielenia się tekstami ze znajomymi. Statystyka nie jest aż tak nudna, jak się nam czasem wydaje.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska