Średnia arytmetyczna pojawiła się w jednym z pierwszych wpisów na moim blogu. Potem było kilka słów o średniej trymowanej, a następnie dłuższa przerwa od średnich. Dzisiaj chciałabym wrócić do tego tematu i przedstawić Wam średnią harmoniczną. Oprócz wzoru i obliczeń, pojawią się również przykłady z życia, kiedy intuicyjne użycie średniej arytmetycznej okazuje się błędem. Czy chcecie się dowiedzieć, po co fizykowi i rowerzyście średnia harmoniczna? Zapraszam do lektury.

Średnia harmoniczna, podobnie jak średnia arytmetyczna, jest klasyczną miarą położenia. Używamy ją w sytuacjach, gdy dane są przedstawione w postaci względnej. Może najpierw kilka przykładów: prędkość – przedstawiana w kilometrach na godzinę. Albo pracochłonność w minutach na sztukę. I jeszcze spożycie w kilogramach na osobę albo cena jednostowa w złotych na sztukę. Przykłady można by było mnożyć, ale chodzi o sytuację, gdy wartości cechy przedstawiamy w przeliczeniu na stałą jednostkę innej zmiennej. Hipotetyczny rowerzysta może jechać z prędkością 10 kilometrów na godzinę albo 15 kilometrów na godzinę. Wartość jego prędkości przedstawiamy za każdym razem w przeliczeniu na jedną godzinę (jest to stała jednostka – zawsze podajemy prędkość w km/godz).

Wzór na średnią harmoniczną wygląda następująco:

\(\overline{x}_{H}=\frac{n}{\sum_{i=1}^{n}\frac{1}{x_{i}}}=\frac{n}{\frac{1}{x_{1}}+\frac{1}{x_{2}}+\ldots+\frac{1}{x_{n}}}\)

Spróbujmy obliczyć średnią harmoniczną dla trzech liczb: 2, 3 i 4.

\(\overline{x}_{H}=\frac{3}{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}}=\frac{3}{\frac{6}{12}+\frac{4}{12}+\frac{3}{12}}=\frac{3}{\frac{13}{12}}=3*\frac{12}{13}=\frac{36}{13}=2,77\)

Zdecydowanie wygląda to dużo mniej przyjaźnie i dużo mniej intuicyjnie niż obliczanie średniej arytmetycznej (dla przypomnienia – w przypadku średniej arytmetycznej byśmy musieli zsumować te trzy liczby (2+3+4) i następnie podzielić przez liczbę elementów, czyli 3. Wynik to 9/3 czyli 3). Dlaczego więc nie mozna poprzestać na obliczaniu średniej arytmetycznej? Dlaczego trzeba sobie komplikować życie i używać wzorów, które u normalnego człowieka wywołują zniechęcenie?

średnia harmoniczna – przykład rowerzysty

Obiecałam wyjaśnienia dla rowerzystów więc niech rowerzysta będzie naszym przykładem. Jedzie on sobie codziennie rano do pracy. Wstaje rześki, pełen sił i wskakuje na rower. Ma do pracy 20 kilometrów i energicznie pedałując rusza z średnią prędkością 20 km/godz. Po godzinie jest w pracy, gdzie dzielnie przez kolejne 8 godzin analizuje skomplikowane zagadnienia statystyczne. Po takich 8 godzinach wysiłku umysłowego jest na tyle zmęczony, że droga powrotna zajmuje mu dwie godziny – jedzie sobie spokojnie z prędkością 10 km/godz. Jaka jest średnia prędkość naszego rowerzysty?

Spróbujmy najpierw wykorzystać naszą intuicyjną średnią arytmetyczną. W jedną stronę 20 km/godz. W drugą stronę 10 km/godz. Odpowiedź nasuwa się jednoznacznie: 15 km/godzinę. Zastanówmy się, co nam powinno pokazać, że to intuicyjne myślenie jest błędne. Skoro rowerzysta w sumie przejechał 40 kilometrów z prędkością 15 kilometrów na godzinę, to powinno mu to zająć 40/15 godziny, czyli 2 godziny i 40 minut. A my przecież wiemy, że jechał przez 3 godziny. Czyli co? Czyli użyliśmy nie tą średnią, która powinna być użyta.

Policzmy więc średnią harmoniczną:

\(\overline{x}_{H}=\frac{2}{\frac{1}{20}+\frac{1}{10}}=\frac{2}{\frac{1}{20}+\frac{2}{20}}=\frac{2}{\frac{3}{20}}=2*\frac{20}{3}=\frac{40}{3}=13\frac{1}{3}\approx13,3\)

Średnia harmoniczna wynosi 13,3 km/godz. Sprawdźmy, czy to się zgadza? Rowerzysta przejechał 40 km ze średnią prędkością 13,3 km/godz. \(\frac{40}{13,3}\) to 3 godziny. I dokładnie tyle czasu potrzebował nasz rowerzysta na przejechanie swojej trasy.

średnia harmoniczna – przykład dla fizyka

Wszystkich fizyków proszę o wyrozumiałość (jeśli pojawią się jakieś nieścisłości), bo ostatni raz miałam ten przedmiot w szkole średniej, czyli lata całe temu. A przykład mój będzie dotyczył rezystorów. Rezystory można połączyć na dwa sposoby: szeregowo albo równolegle.

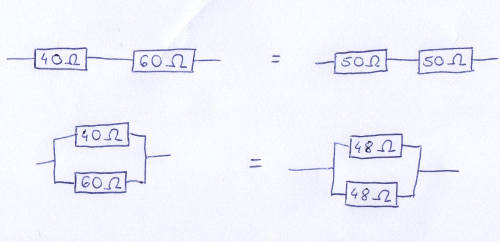
Jeśli dwa rezystory 40Ω i 60Ω połączymy szeregowo i będziemy chcieli je zastąpić dwoma rezystorami o tym samym oporze, to do obliczenia wymaganego oporu używamy średniej arytmetycznej (czyli dwa rezystory 40Ω i 60Ω możemy zastąpić dwoma rezystorami o oporze 50Ω).

Jeśli jednak rezystory te będą połączone równolegle, to musimy wykorzystać średnią harmoniczną, która wyniesie 48Ω. Dwa rezystory o oporze 40Ω i 60Ω połączone równolegle można zastąpić dwoma rezystorami o oporze 48Ω każdy.

\(\overline{x}_{H}=\frac{2}{\frac{1}{40}+\frac{1}{60}}=\frac{2}{\frac{6}{240}+\frac{4}{240}}=\frac{2}{\frac{10}{240}}=2*\frac{240}{10}=48\)

Zapraszam do lektury kolejnego tekstu, w którym można poznać jeszcze inne przykłady średniej harmonicznej i dowiedzieć się, co wspólnego ma średnia harmoniczna z trapezem. Zapraszam do lektury.

Zaproście również swoich znajomych – zarówno tych, którzy lubią statystykę, jak i tych, którzy dotychczas uważali, że jest niepotrzebna, niezrozumiała i w ogóle do niczego.

 

---

Droga Czytelniczko! Drogi Czytelniku!

Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.

Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.

A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.

Pozdrawiam Cię serdecznie i życzę miłego dnia!

Krystyna Piątkowska