Ludzie wcale nie pochodzą od małp. Dzielą z nimi podobno tylko 95% DNA. Z piratami dzielą 99,9% i to oni są naszymi przodkami. Tak w każdym razie twierdzą wyznawcy Latającego Potwora Spaghetti. Konsekwencją spadku liczby piratów jest globalne ocieplenie. Żeby to udowodnić, pastafarianie przedstawili wykres, z którego wyraźnie wynika korelacja pomiędzy temperaturą, a liczbą piratów. Wykres nie budzi żadnych wątpliwości. Cóż więc robić? Przyłączyć się do pastafarian i zrewidować swoje dotychczasowe poglądy religijne, czy może lepiej zrozumieć, co to jest korelacja? Dziś przedstawimy współczynnik korelacji Pearsona.
co to jest korelacja
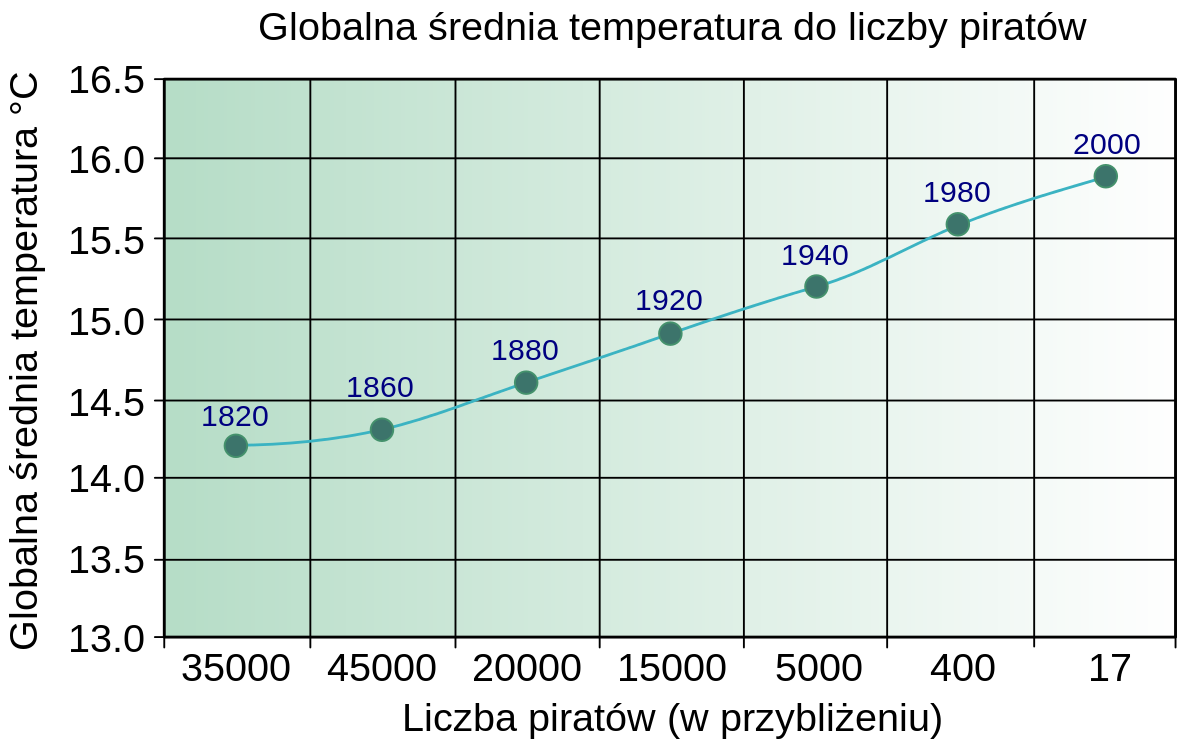
Wykres zaprezentowany przez pastafarian wygląda następująco:
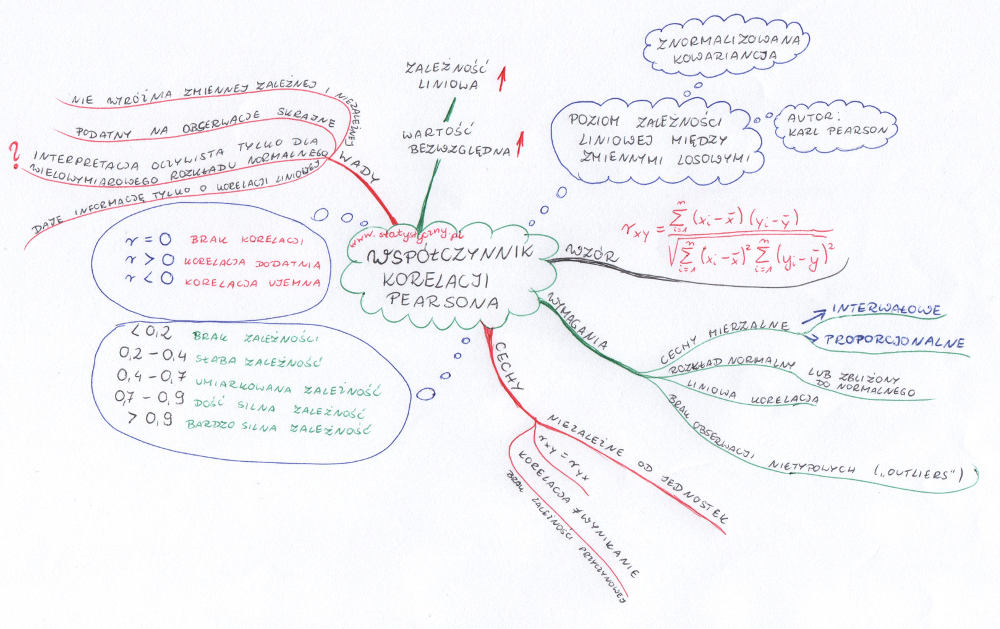
Jak widać, liczba piratów maleje, a temperatura rośnie. Czyli co? Należy kupić żaglowiec, przyczepić czarną flagę na maszcie i ruszyć w świat? Do tego, czy rzeczywiście piraci mają wpływ na globalne ocieplenie jeszcze wrócimy, a tymczasem zastanówmy się, co to w ogóle jest korelacja i jak ją możemy mierzyć. Korelacja to inaczej współzależność, która występuje pomiędzy dwoma zjawiskami. W statystyce poziom zależności liniowej między dwoma zmiennymi losowymi mierzy się za pomocą współczynnika korelacji liniowej Pearsona. A współczynnik ten obliczamy za pomocą wzoru:
\(r_{xy}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}\sum_{i=1}^{n}(y_{i}-\overline{y})^{2}}}\)Wzór ten po różnych przekształceniach może wyglądać zupełnie inaczej – nie należy się zdziwić, jak zobaczymy go w trochę innej formie.
Na przykład w takiej:
\(r_{xy}=\frac{\sum_{i=1}^{n}x_{i}y_{i}-n\overline{x}\overline{y}}{n\sigma_{x}\sigma_{y}}\)gdzie \( \sigma_{x}\) i \(\sigma_{y}\) oznaczają odchylenia standardowe
albo w takiej:
\(r_{xy}=\frac{\sum_{i=1}^{n}x_{i}y_{i}-\sum_{i=1}^{n}x_{i}\sum_{i=1}^{n}y_{i}}{\sqrt{n\sum_{i=1}^{n}x_{i}^{2}-(\sum_{i=1}^{n}x_{i})^{2}}\sqrt{n\sum_{i=1}^{n}y_{i}^{2}-(\sum_{i=1}^{n}y_{i})^{2}}}\)
wartości współczynnika korelacji Pearsona
Współczynnik korelacji Pearsona to znormalizowana kowariancja. Obliczony wynik zawsze mieści się w przedziale od -1 do 1. Jeśli współczynnik wynosi zero (r=0), to wiemy, że mamy do czynienia z brakiem korelacji liniowej pomiędzy dwoma cechami. Jeśli wynik jest dodatni (r>0), to znaczy, że mamy do czynienia z korelacją dodatnią. Wraz ze wzrostem wartości jednej cechy można spodziewać się wzrostu wartości drugiej cechy. W przypadku ujemnych wartości współczynnika (r<0), mówimy o korelacji ujemnej. Czyli dla wyższych wartości jednej cechy można spodziewać się spadku wartości drugiej cechy.
Jeśli chodzi o poziom zależności, to dla wartości bezwględnych można przyjąć następujące założenia:
<0,2 brak zależności
0,2-0,4 słaba zależność
0,4-0,7 umiarkowana zależność
0,7-0,9 dość silna zależność
>0,9 bardzo silna zależność
W różnych opracowaniach przedziały te mogą się trochę różnić, ale mniej więcej wiadomo, jakie wartości mówią o zależności pomiędzy badanymi zmiennymi. Dodajmy tutaj, że inne wartości będą miały znaczenie dla badaczy z różnych dziedzin. Często jest tak, że w naukach np. psychologicznych czy ekonomicznych dużo niższe wartości uznawane są za silną zależność niż w precyzyjnych naukach fizycznych albo chemicznych.
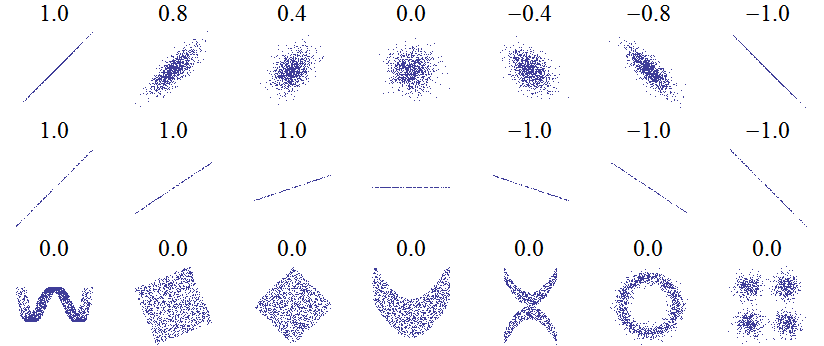
Chciałam jeszcze Wam pokazać jeden rysunek, który pokazuje wartości współczynnika korelacji liniowej Pearsona dla różnych danych:
Są to przykładowe wykresy danych (x, y) i odpowiadające im wartości współczynnika korelacji liniowej Pearsona. Mnie się najbardziej podoba ostatni rządek, który przedstawia bardzo ciekawe kształty. Wyraźnie jest tam jakaś korelacja pomiędzy danymi. Ale ponieważ korelacja ta nie jest liniowa, to współczynnik Pearsona nic nam tu nie pomoże.
Drugi rządek też jest bardzo ciekawy. Pokazuje, że na wartość współczynnika korelacji nie ma wpływu nachylenie krzywej pokazującej zależność między wartościami x i y. Liczy się tylko, jak bardzo są one rozproszone (pierwszy rząd wykresów).
założenia
Żeby liczyć współczynnik korelacji musimy pamiętać o kilku podstawowych założeniach. Przede wszystkim musimy mieć do czynienia z cechami mierzalnymi. W ostatnim wpisie omawiałam podział cech zaproponowany przez Stanleya Smitha Stevensa mówiąc, że jest on istotny, żebyśmy mogli stwierdzić, czy dla danej cechy możemy obliczać jakiś wskaźnik statystyczny. Współczynnik korelacji Pearsona możemy liczyć dla cech interwałowych (ang. interval) oraz proporcjonalnych (ang. ratio). Czyli nie liczymy go dla płci, poziomu zadowolenia ani koloru oczu. Za to możemy sprawdzać korelację pomiędzy temperaturą wyrażoną w stopniach Celsjusza a czasem, który dana osoba jest w stanie wytrwać na ogrodowym leżaku. Kolejne wymaganie jest takie, że cecha musi mieć rozkład normalny lub zbliżony do normalnego. Pamiętajmy również, że współczynnik korelacji Pearsona liczy korelację liniową. Jeśli narysujemy sobie wykres i na pierwszy rzut oka widać, że korelacja jakaś jest, ale z liniową nie ma nic wspólnego, to nie warto się męczyć z obliczeniami. Jeśli mamy również do czynienia z obserwacjami nietypowymi, mocno odstającymi od reszty, to zakłócą one wynik i obliczony współczynnik korelacji nie będzie zbyt wiele wart.
Czyli co? Czyli zakładamy, że mamy do czynienia z cechami ilościowymi, charakteryzującymi się przepięknym rozkładem normalnym, bez żadnych wartości nietypowych – w takiej sytuacji można szukać korelacji liniowej.
Korelacja a wynikanie
Ale uwaga! Pamiętajmy, że korelacja i wynikanie to zupełnie dwie inne sprawy, jakże często mylone przez większość ludzi. W statystyce, kiedy mówimy o korelacji, to opisujemy siłę oraz kierunek relacji między dwoma zmiennymi (albo większą ich liczbą). Jesli natomiast mówimy o wynikaniu, to wiemy, że wpływając na jedną zmienną, równocześnie wpływamy na drugą zmienną. Są one ze sobą powiązane. Ale żeby potwierdzić, że tak się dzieje, trzeba przeprowadzić nie tylko obserwację, ale przede wszystkim eksperyment, który będzie uwzględniał grupę obserwowaną, grupę kontrolną itp. Temat wymagałby osobnego wpisu, więc tylko sygnalizuję problem. Myślę, że kiedyś do niego wrócę i wtedy dokładniej będę wyjaśniać, kiedy możemy mówić o wynikaniu. Dodam tylko, że w języku angielskim jest bardzo znane powiedzienie: „Correlation does not imply causation”. Jest ono źródłem wielu żartów:

źródło: xkcd.com
I właśnie często za jedną z wad współczynnika korelacji uważa się, że nie wyróżnia on zmiennej zależnej i niezależnej. Mówi o relacji między dwoma cechami, a nie określa, czy jedna z nich jest źródłem drugiej czy nie.
Wróćmy więc na chwilę do naszego Latającego Potwora Spaghetti i do piratów wpływających na globalne ocieplenie. I owszem, występuje między nimi korelacja, ale nie możemy powiedzieć nic na temat wpływu jednego i drugiego. Możemy mieć do czynienia z zupełnie innymi zmiennymi, które mają wpływ na liczbę piratów i jeszcze innymi zmiennymi, które wpływają na średnią temperaturę. Ich działanie wywołuje taki efekt, jakby piraci i globalne ocieplenie miały coś ze sobą wspólnego, nawet jeśli nie ma żadnego eksperymentu, który by mógł potwierdzić takie stwierdzenie. Korelacja – tak, wynikanie – nie. Swoją drogą, bardzo jednostronni ci pastafarianie. Dlaczego twierdzą, że liczba piratów ma wpływ na globalne ocieplenie? A może to wraz ze wzrostem temperatur masowo wymierają piraci? Może ktoś się pokusi o eksperymenty w tym temacie 😉
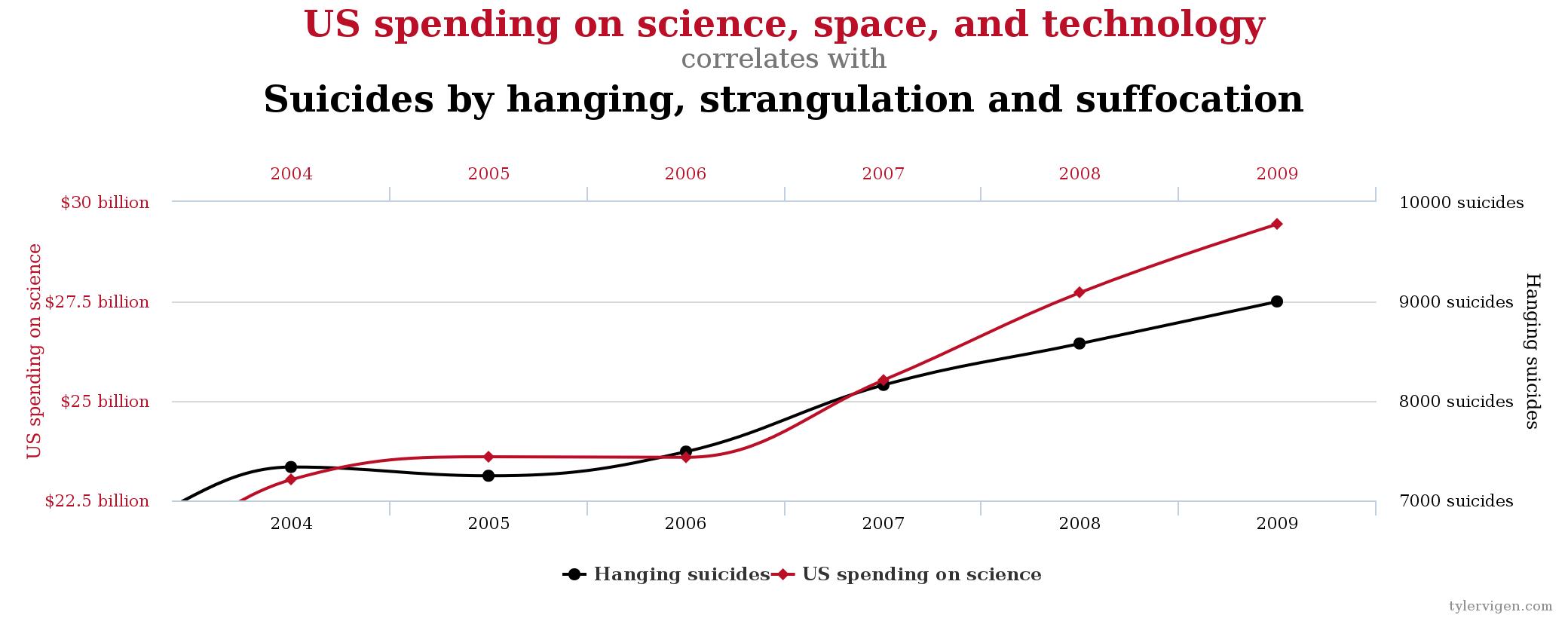
A jeśli chodzi o nietypowe korelacje to jednym z najbardziej znanych „wyszukiwaczy” takich powiązań jest Tyler Vigen. Proponuję spojrzeć na jego wykres przedstawiający powiązanie „wydatków USA na naukę, badanie kosmosu i technologie” oraz „samobójstwa przez powieszenie lub uduszenie”. Obliczony przez Vigena współczynnik korelacji wynosi 99,79%. Przecież to korelacja niemalże doskonała.
źródło: www.tylervigen.com
Od tego momentu proszę więc uważnie pilnować, czy dane, które analizujecie świadczą tylko o korelacji czy o wynikaniu. Wyobraźmy sobie sytuację w firmie. Pan Karol postanowił przejść na dietę i przez dwa miesiące chudł kilogram na tydzień. Do pracy została przyjęta Pani Halinka, która słodzi herbatę pięcioma łyżeczkami cukru. W efekcie waga Pana Karola spada, a zużycie cukru w firmie rośnie. Jest korelacja między tymi dwoma zmiennymi, ale nie uwględnia ona dodatkowej zmiennej w postaci pełnej cukru herbaty Pani Halinki.
Albo jeszcze inny przykład. Firma produkująca sprzęt sportowy ma kłopoty finansowe. W związku z tym kierownik wzywa na dywanik szefa działu marketingu. Ten przeznacza dodatkowe 10% budżetu na reklamę w telewizji. Po miesiącu okazuje się, że sprzedaż wzrosła i to o 20%. Dumny szef działu marketingu przedstawia kierownikowi wykres – jest wyraźna korelacja pomiędzy nakładami na reklamę w telewizji i wzrostem sprzedaży. Nikt nie zauważył, że w tym samym czasie znany bloger napisał artykuł o sprzęcie sportowym tej właśnie firmy, zachęcając do zakupu wszystkich swoich czytelników. Korelacja i owszem wystąpiła, ale powód wzrostu sprzedaży był zupełnie inny niż reklama telewizyjna.
I nawet jeśli nie zapamiętacie z tego artykułu wzoru na współczynnik korelacji Pearsona, jeśli nie będziecie umieli go obliczyć, jeśli nie będziecie wiedzieli, jakie wartości może przyjmować i co one oznaczają… Zapamiętajcie jedno: Korelacja zjawisk nie musi oznaczać ich związku przyczynowo-skutkowego. Nie wkładajcie więc durszlaka na głowę, nie kupujcie pirackiego statku. Jest spora szansa, że wyznawcy Latającego Potwora Spaghetti jednak się mylą…
Ciąg dalszy rozważań na temat współczynnika korelacji (w tym liczne przykłady) w kolejnym wpisie – zapraszam!
Przypominam wszystkim przy okazji, że statystyczny ma już swój fanpage na Facebooku – warto polubić. Jeśli uważacie, że piszę coś ciekawego, to podzielcie się ze znajomymi. Nie dajcie się robić w bambuko ludziom, którzy rozumieją statystykę lepiej niż Wy 🙂
PS. Ktoś zauważył, że sama wpadłam w pułapkę? W drugim przykładzie napisałam „powód wzrostu sprzedaży był zupełnie inny niż reklama telewizyjna”. Powinno być „mógł być zupełnie inny”, bo nie było eksperymentu i nie wiemy, czy reklama miała wpływ na sprzedaż czy nie miała.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska