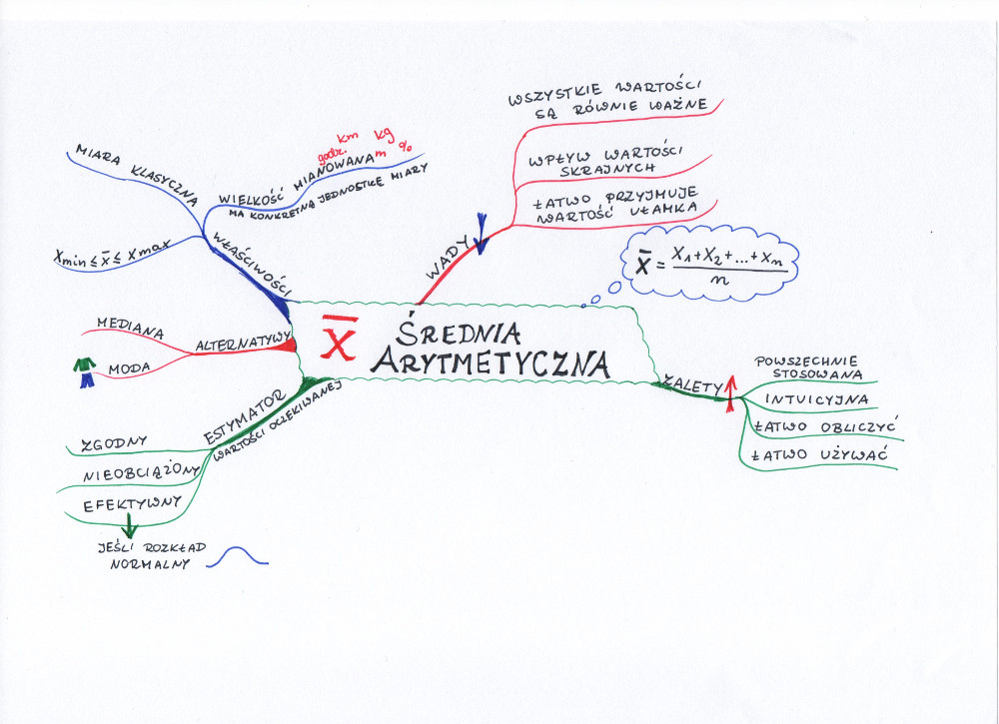
Mam wrażenie, że najbardziej znanym pojęciem statystycznym jest średnia arytmetyczna. Na pewno każdy wiele razy słyszał, ile wynoszą średnie zarobki, liczył średnią ocen w szkole albo zastanawiał się, jakie jest średnie zużycie paliwa w samochodzie.
Co to jest właściwie ta średnia i jak ją można policzyć? Czy jej znaczenie jest zawsze oczywiste?
Średnią arytmetyczną otrzymujemy poprzez zsumowanie wartości wszystkich badanych obiektów i podzielenie tej sumy przez liczbę obiektów.
\(\overline{x}=\frac{x_{1}+x_{2}+…+x_{n}}{n}\)
Najbardziej klasyczny przykład, znany od szkoły podstawowej, to liczenie średniej ocen. Mamy pięć przedmiotów: język polski, matematykę, język angielski, przyrodę oraz wychowanie fizyczne. Uczeń dostał odpowiednio następujące oceny na koniec semestru: 4, 5, 2, 4, 5. Jak liczymy średnią arytmetyczną? Poprzez dodanie do siebie poszczególnych ocen (4+5+2+4+5), a następnie podzielenie przez liczbę przedmiotów. 20/5 to 4. Nasze obliczenia wskazują więc, że średnia ocen ucznia wynosi 4.
Jak widać z przykładu, średnią arytmetyczną liczy się bardzo łatwo, szczególnie gdy mamy dostęp do wszystkich wartości. Jest intuicyjna, łatwo się ją interpretuje, łatwo używa i dzięki temu właśnie jest powszechnie stosowana – niestety, również w sytuacjach, kiedy nie powinna.
Wady średniej arytmetycznej
Średnia arytmetyczna ma kilka poważnych wad, na które warto zwrócić uwagę:
- Przede wszystkim jest to duży wpływ wartości skrajnych. Załóżmy, że chcemy sprzedać na allegro książkę i analizujemy ceny sprzedaży z przeszłości. Jeśli w większości przypadków cena książki wynosiła 20-25 zł, a równocześnie jeden egzemplarz poszedł za 2000 zł (bo miał autograf autora i został zakupiony przez pasjonata), to kwota 2000 zł bardzo istotnie zawyży średnią wartość książki.
- Średnia łatwo przyjmuje wartości ułamka, nawet w sytuacjach, kiedy ułamkowa wartość nigdy nie ma prawa wystąpić w rzeczywistości. Taki na przykład współczynnik dzietności, który dla Polski w 2013 roku wyniósł 1,32 i oznacza liczbę urodzonych dzieci przypadających na jedną kobietę w wieku rozrodczym. Z jednej strony wiadomo, jak interpretować tę liczbę (oj, mało dzieci rodzimy, niestety), ale równocześnie zdajemy sobie sprawę z faktu, że nie ma żadnej kobiety, która urodziłaby 1,32 dziecka.
- Wszystkie wartości są tak samo ważne i mają identyczny wpływ na wynik. Jeśli naszym celem by była analiza przedmiotów zmieniających się w czasie i chcielibyśmy największą wagę nadać wartościom najnowszym, to niestety średnia arytmetyczna się nie przyda. Wróćmy do przykładu sprzedaży książki na allegro. Jeśli mamy dane odnośnie cen z ostatnich 5 lat, to możemy chcieć uwzględnić wszystkie wartości, ale równocześnie większą wagę przypisać kwotom z ostatniego roku. W takiej sytuacji zwykła średnia arytmetyczna nie znajdzie swojego zastosowania.
Psi przykład
Słyszeliście na pewno słynne powiedzenie, że skoro ja mam dwie nogi, a mój pies cztery, to średnio mamy po trzy nogi. Jest ono bardzo często wypowiadane przez osoby, które nie rozumieją statystyki, nie wiedzą, kiedy jej użyć i jak wykorzystać obliczone wartości. Ma pokazać, że statystyka przekłamuje rzeczywistość. Zdanie to jest jak najbardziej prawdziwe. Sumujemy 2+4 i otrzymujemy 6. Następnie dzielimy przez liczbę badanych jednostek (2) i jak by nie patrzeć wynik wychodzi 3. Ale czy właśnie taki wynik chcieliśmy otrzymać? Czy interesuje nas średnia liczba nóg jednego psa i jednego człowieka? Mają oni reprezentować wszystkie psy i wszystkich ludzi? Mieszkańców naszego osiedla? Czy może wszystkie ssaki na ziemi? Po co liczymy średnią nóg dwóch zupełnie różnych stworzeń?
Odchodząc trochę od tematu (dla zupełnych laików – proszę bez paniki! Temat odchylenia standardowego i typowego obszaru zmienności pojawi się już wkrótce – na razie potraktujcie to z dystansem), warto spojrzeć nie tylko na samą średnią, ale na inne miary, które w pewien sposób są z nią powiązane. Na przykład odchylenie standardowe. W naszym przypadku psa i człowieka wynosi ono dokładnie 1. Pójdźmy dalej. Typowy obszar zmienności, w którym znajduje się teoretycznie około 2/3 badanych obiektów (pod pewnymi założeniami, oczywiście) mieści się w przedziale od 2 do 4 (od średniej arytmetycznej odejmujemy odchylenie standardowe, żeby otrzymać dolną granicę i dodajemy ochylenie standardowe, żeby otrzymać górną granicę). Czyli co? Czyli i nasz pies i jego właściciel zmieścili się w typowym obszarze zmienności. Nie jest więc aż tak źle z tą naszą statystyką, mimo że przykład bezsensowny i nasze obliczenia mogą tylko służyć obaleniu niezbyt mądrego argumentu, że statystyka jest zła.
(Swoją drogą – ciekawy tekst o przykładzie trzech nóg człowieka i psa można znaleźć też tutaj.)
Przykład średniego wynagrodzenia
A teraz przejdźmy do czegoś bardziej przydatnego. Firma rekrutuje pracowników i jako jeden z argumentów zachęcających podaje: „średnie wynagrodzenie w naszej firmie wynosi 5000 zł”. Brzmi kusząco, prawda? Ale czy jest to dla nas informacja wystarczająca? Czy powie nam, ile w rzeczywistości wyniosą nasze zarobki?
Załóżmy, że mamy cztery firmy:
- „Wszystkim Równo” – zatrudnia 10 pracowników, z których każdy dostaje co miesiąc 5000 zł.
- „Szefo Górą” – zatrudnia panią sprzątaczkę, która na umowę zlecenie otrzymuje 500 zł, do tego 8 szeregowych pracowników z pensją 1500 zł i kierownika, który co miesiąc na konto przyjmuje 37500 zł.
- „Byle do Awansu” – mamy tu również 10 pracowników – pięciu pracuje poniżej roku i otrzymują 3000 zł, druga piątka ma już dłuższy staż i dzięki temu doczekała się pensji po 7000 zł.
- „Wielka Niewiadoma” – dziesięciu pracowników, każdy z inną pensją, od 1000 do 9000 zł.
W każdej z powyższych firm średnia wynagrodzenia wynosi 5000 zł. Na pewno nie w każdej z nich byśmy chcieli pracować. Czyli w takim przypadku średnie wynagrodzenie to informacja absolutnie niewystarczająca.
Przykład – torebki z mąką
Po tych dwóch przykładach, które wskazują, jak niedoskonała jest średnia arytmetyczna, chciałam pokazać sytuację, gdzie wykorzystanie średniej jest jak najbardziej uzasadnione. Załóżmy, że mamy młyn, w którym ładujemy mąkę do kilogramowych torebek. No i po całym dniu chcielibyśmy sprawdzić, czy w torebkach rzeczywiście wylądował kilogram mąki. W związku z czym ważymy wszystkie torebki z mąką i okazuje się, że tylko niektóre ważą dokładnie 1000 gram. Są torebki lżejsze i cięższe. Ale jak się przekonać, czy sumarycznie nasypaliśmy za dużo, czy za mało? Właśnie tutaj przyda się obliczenie średniej arytmetycznej. Intuicyjnie się domyślamy, że mamy do czynienia z jednorodną zbiorowością, w której nie powinno być zbyt wiele wartości skrajnych (czy tak jest na pewno? – to też warto sprawdzić), wszystkie wartości są dla nas tak samo ważne, a wynik w postaci ułamka nam nie przeszkadza. Wszystkie przesłanki do użycia średniej arytmetycznej są więc spełnione.
Macie swoje pomysły, kiedy warto liczyć średnią arytmetyczną, a kiedy podawanie jej wartości jest bezsensowne? Może jakieś przykłady? Zachęcam do dzielenia się w komentarzach.
A mój przykład rzeczywistego i codziennego wykorzystania średniej arytmetycznej pojawi się w kolejnym wpisie. Zapraszam do czytania.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska