Obliczenie średniej arytmetycznej to czasem za mało. Co z tego, że znamy średnie wynagrodzenie w firmie (wynoszące – jak w naszym przykładzie np. 5000 zł), skoro nie wiemy jaka jest zmienność wynagrodzenia? Czy wszyscy pracownicy dostają dokładnie tyle samo? A może kierownik zawyża wartość średniej pensji? Zapraszam do lektury tekstu o odchyleniu standardowym. Jest to jedno z narzędzi, które pozwala przeanalizować rozproszenie wartości wokół średniej.
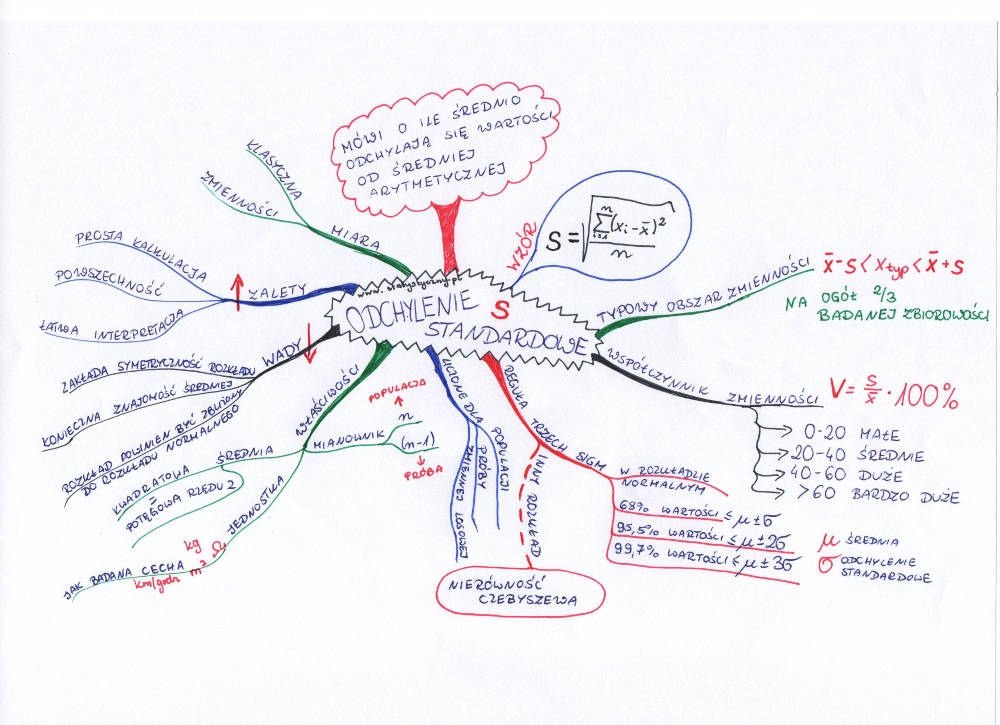
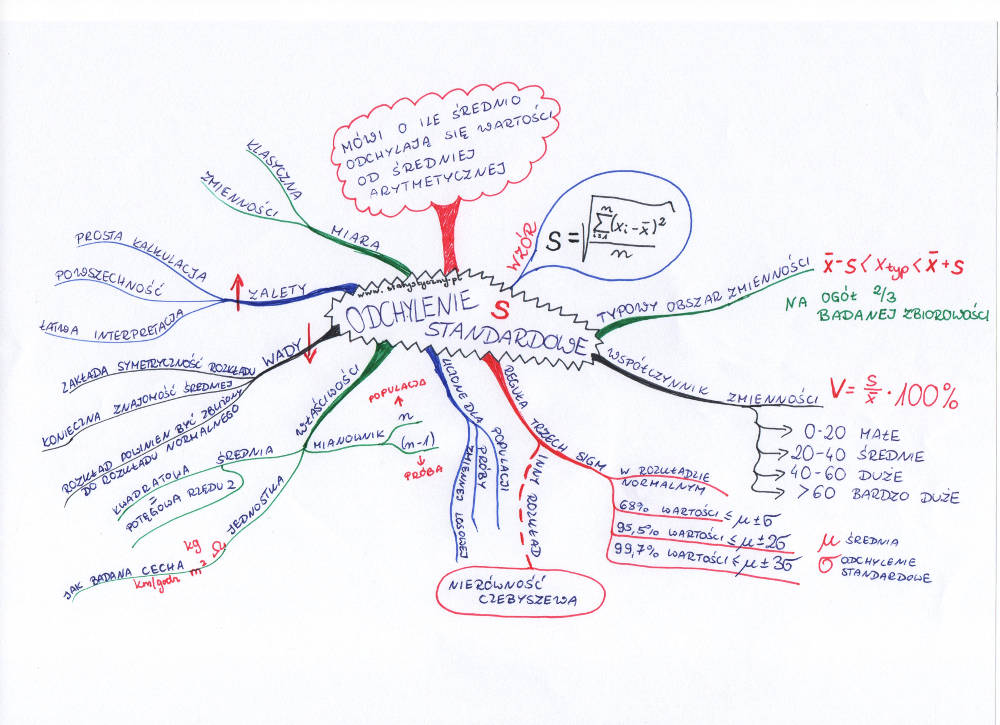
Odchylenie standardowe mówi o tym, o ile średnio odchylają się wartości badanej cechy od średniej arytmetycznej. Brzmi trochę jak masło maślane, prawda? Średnio od średniej? Co to ma znaczyć?
Zaraz opowiem. Znacie już różne średnie: arytmetyczną, harmoniczną i geometryczną. I tu taki psikus – odchylenie standardowe nie jest liczone za pomocą którejkolwiek z tych średnich. Używa się zupełnie innej – średniej kwadratowej. Średnia kwadratowa to średnia potęgowa stopnia 2 (średnia harmoniczna to -1 stopnia, geometryczna to 0 stopnia, arytmetyczna to 1 stopnia). I ta właśnie średnia jest potrzebna, żeby obliczyć odchylenie standardowe. A jak to robimy? Zaraz wszystko opiszę i pokażę przykłady. Mam nadzieję, że wtedy już wszystko będzie zrozumiałe.
Na początku obliczamy średnią arytmetyczną – będzie nam za chwilę potrzebna. Potem po kolei obliczamy różnicę między wartością cechy każdej zaobserwowanej jednostki, a średnią arytmetyczną. Następnie każdą z różnic podnosimy do kwadratu i wszystko sumujemy ze sobą. Na koniec dzielimy przez liczbę obserwacji i wyciągamy pierwiastek drugiego stopnia z otrzymanego wyniku. I w ten sposób obliczyliśmy odchylenie standardowe.
A teraz to samo, ale zapisane za pomocą wzoru matematycznego:
\(s=\sqrt{\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}{n}}=\sqrt{\frac{(x_{1}-\overline{x})^{2}+(x_{2}-\overline{x})^{2}+\ldots+(x_{n}-\overline{x})^{2}}{n}}\)(ponieważ jest to „odchylenie standardowe dla początkujących”, to nie będę tłumaczyć szczegółów, ale tylko w dwóch słowach wspomnę, że gdybyście liczyli odchylenie standardowe z próby, a nie z populacji, to zamieńcie w mianowniku n na (n-1))
Odchylenie standardowe jest klasyczną miarą zmienności rozkładu. Liczymy je po to, żeby stwierdzić, czy w naszej populacji jednostki są podobne ze względu na badaną cechę, czy znacznie różnią się między sobą.
Załóżmy najprostszy przykład – mamy 3 liczby: 1, 2 i 3. Średnia arytmetyczna tych trzech liczb to 2 (liczona wzorem: \(\frac{1+2+3}{3}\)). Odchylenie standardowe liczymy następująco:
\(s=\sqrt{\frac{(1-2)^{2}+(2-2)^{2}+(3-2)^{2}}{3}}=\sqrt{\frac{1+0+1}{3}}=\sqrt{\frac{2}{3}}\approx0,82\)Współczynnik zmienności
Jak znamy już odchylenie standardowe, to możemy obliczyć różne inne miary rozproszenia, na przykład współczynnik zmienności:
\(V=\frac{s}{\overline{x}}*100\%\)Jeśli współczynnik zmienności waha się w przedziale 0-20%, to zróżnicowanie populacji jest małe. Jeśli znajduje się w przedziale 20-40%, to mówi się o średnim zróżnicowaniu populacji. W przypadku 40-60% mamy do czynienia z dużym zróżnicowaniem. Kiedy natomiast współczynnik zmienności przekroczy wartość 60%, to oznacza, że zróżnicowanie jest bardzo duże.
Dla naszego przykładu trzech liczb 1, 2 i 3 wyniesie on:
\(V=\frac{0,82}{2}*100\%=41\%\)Wynik 41% oznacza, że zróżnicowanie w naszym przykładzie jest duże.
Typowy obszar zmienności
Po obliczeniu odchylenia standardowego i średniej arytmetycznej, można również wyliczyć sobie tzw. typowy obszar zmienności:
\(\overline{x}-s<x_{typ}<\overline{x}+s\)W naszym przykładzie:
\(2-0,82<x_{typ}<2+0,82\)Oznacza to, że typowy obszar zmienności zawiera się w zakresie od 1,18 do 2,82.
W dużym uproszczeniu mówi się, że typowy obszar zmienności zawiera 2/3 badanej zbiorowości. Jest to uproszczenie dlatego, że uwzględnia niepisane założenie, że mamy do czynienia z rozkładem normalnym lub rozkładem zbliżonym do normalnego (co to jest ten rozkład normalny, to temat na dłuższą wypowiedź i nie będę chwilowo tłumaczyć). Dodam więcej. Jeśli nasze dane pochodzą z populacji o rozkładzie normalnym, to 68% zbiorowości zawiera się w odległości jednego odchylenia standardowego od średniej arytmetycznej. W odległości 2 odchyleń standardowych zawiera się 95,5% obserwowanych jednostek. Natomiast w odległości 3 odchyleń standardowych zawiera się 99,7% badanej populacji. Są to bardzo istotne informacje, ponieważ na nich opiera się wiele hipotez statystycznych i na pewno wielokrotnie będziemy wracać do tego tematu.
A co w sytuacji, kiedy wiemy, że nasza populacja nie ma nic wspólnego z rozkładem normalnym? Wtedy przyjmuje się trochę bardziej restrykcyjne warunki – wynikające z nierówności Czebyszewa. Przyjmuje się, że w odległości dwóch odchyleń standardowych od średniej zawiera się 75% obserwacji, w odległości 3 odchyleń zawiera się 88,89% obserwacji, w odległości 4 odchyleń – 93,75% obserwacji, natomiast w odległości 5 odchyleń standardowych od średniej zawiera się 96% obserwacji.
Przykład średniego wynagrodzenia
I po raz kolejny wróćmy do naszego przykładu ze średnim wynagrodzeniem:
- „Wszystkim Równo” – zatrudnia 10 pracowników, z których każdy dostaje co miesiąc 5000 zł.
- „Szefo Górą” – zatrudnia panią sprzątaczkę, która na umowę zlecenie otrzymuje 500 zł, do tego 8 szeregowych pracowników z pensją 1500 zł i kierownika, który co miesiąc na konto przyjmuje 37500 zł.
- „Byle do Awansu” – mamy tu również 10 pracowników – pięciu pracuje poniżej roku i otrzymują 3000 zł, druga piątka ma już dłuższy staż i dzięki temu doczekała się pensji po 7000 zł.
- „Wielka Niewiadoma” – dziesięciu pracowników, każdy z inną pensją, od 1000 do 9000 zł.
Przypominam, że we wszystkich powyższych przykładach średnie wynagrodzenie wynosi 5000 zł (liczone za pomocą średniej arytmetycznej). A ja udowadniam, że sama informacja o średnim wynagrodzeniu to za mało, żeby świadomie wybrać, w której firmie chcielibyśmy pracować. Zastanówmy się więc, jak tu wygląda kwestia odchylenia standardowego, typowego obszaru zmienności (pomijając temat normalności rozkładu) oraz współczynnika zmienności?
W firmie „Wszystkim Równo” odchylenie standardowe wynosi dokładnie 0. Współczynnik zmienności to również 0 i dowiadujemy się w ten sposób (tylko z informacji o średniej arytmetycznej i odchyleniu standardowym), że wszyscy pracownicy zarabiają dokładnie tyle samo.
W firmie „Szefo Górą” sytuacja jest zupełnie inna. Odchylenie standardowe wynosi 10.837,44 zł. Sporo, prawda? I wszystko za sprawą jednego kierowniczego wynagrodzenia. Współczynnik zmienności przekroczył tu 200%. 10.837,44/5000*100%=216%. A typowy obszar zmienności sięga aż ujemnych wynagrodzeń. Wydaje mi się, że to dobry przykład, żeby unikać klasycznych miar zarówno położenia (średnia arytmetyczna), jak i zmienności (odchylenie standardowe) w sytuacjach, kiedy mamy do czynienia z dużymi wartościami skrajnymi. Przypominam, że mediana jak i rozstęp międzykwartylny (czyli miary pozycyjne) bardzo ładnie pokazywały, jakiego wynagrodzenia moglibyśmy spodziewać się w tej firmie.
W przypadku „Byle do Awansu” odchylenie standardowe wynosi 2000 zł. Współczynnik zmienności to 40% (czyli wynagrodzenie jest na pograniczu średniej i dużej zmienności), a typowe wynagrodzenie, które powinno otrzymywać przynajmniej 2/3 pracowników to wartości pomiędzy 3000 a 7000 (akurat w naszym przypadku wszyscy dostają dokładnie albo 3000 zł albo 7000 zł).
No i jeszcze firma „Wielka Niewiadoma”. Tutaj odchylenie standardowe wynagrodzenia wynosi 2459,67 zł. Współczynnik zmienności wynosi 49% (czyli zmienność wynagrodzenia jest duża), a typowe wynagrodzenie 2/3 pracowników mieści się w przedziale od 2540,33 zł do 7459,67 zł.
Kolejna miara – kolejne informacje. Czy wiecie już, w której firmie byście chcieli pracować?
Kiedy zwracać uwagę na odchylenie standardowe?
Odchylenie standardowe jest (a przynajmniej często powinno być) wykorzystywane w codziennym życiu. Jest uważane między innymi za miarę ryzyka w przypadku inwestycji. Jeśli na giełdzie jedna spółka przyniosła średni roczny zysk 4% a druga średni roczny zysk 5%, to wcale nie znaczy, że lepiej bez zastanowienia wybrać tę drugą spółkę. Pomijając analizę fundamentalną i analizę techniczną dla danej spółki, pomijając sytuację makroekonomiczną w kraju, warto spojrzeć na same wahania notowań. Jeśli wartość akcji pierwszej spółki w ciągu roku miała nieznaczne, kilkuprocentowe wahania, a drugiej wahała się o kilkadziesiąt procent, to logicznym jest, że inwestycja w pierwszą spółkę była dużo mniej ryzykowna. A żeby porównać różne stopy zwrotu i sprawdzić ich ryzykowność, można wykorzystać właśnie odchylenie standardowe. Im większe odchylenie standardowe, tym bardziej ryzykowna inwestycja.
Zauważmy również, że informacja o średniej rocznej temperaturze w danej miejscowości również niewiele nam powie. W Polsce mamy cztery pory roku, temperatury dość mocno różnią się między latem a zimą. Są natomiast kraje, w których temperatura nieznacznie się waha w ciągu roku. Nawet jeśli średnia roczna temperatura będzie porównywalna, to nie oznacza, że mówimy o takim samym klimacie. Tu również można skorzystać z odchylenia standardowego (lub innych miar rozproszenia), żeby sprawdzić, czy temperatury mocno wahają się od średniej, czy raczej niewiele.
Wady i zalety odchylenia standardowego
Jakie zalety ma odchylenie standardowe? Przede wszystkim jest powszechnie stosowane, każdy zainteresowany wie, co to jest i skąd się wzięło. Odchylenie standardowe liczy się dość łatwo (pomimo tych okrutnych sum i pierwiastków we wzorze) i jeszcze łatwiej interpretuje. W statystyce wykorzystywane jest bardzo często. Jeśli tylko chcecie bliżej zaprzyjaźnić się ze statystyką, to chcąc nie chcąc musicie również zaprzyjaźnić się z odchyleniem standardowym. I musicie wybaczyć mu te kilka wad, które również posiada. A wśród nich najważniejsza jest ta, że zakłada symetryczność rozkładu. Odchylenie standardowe najlepiej liczy się wtedy, kiedy nasza badana populacja ma rozkład normalny (lub choć zbliżony do normalnego). I nie zapomnijcie, że aby wyliczyć odchylenie standardowe, najpierw trzeba wyliczyć średnią arytmetyczną.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska