Czy statystyków interesuje symetria? Co oznacza pojęcie współczynnika skośności? Kiedy średnia arytmetyczna jest równa medianie? Jak obliczyć współczynnik asymetrii? O czym informuje nas trzeci moment centralny? O tym i o wielu innych rzeczach można przeczytać w poniższym wpisie. Zapraszam do lektury!
W ostatnich wpisach odeszliśmy mocno od obliczania różnych miar rozkładu. Pora wrócić do tematu, bo miary położenia i rozproszenia to jeszcze nie wszystko. Żeby dobrze zrozumieć dzisiejszy wpis proponuję przypomnieć sobie, co to jest średnia arytmetyczna, mediana, dominanta, odchylenie standardowe, kwartyle oraz odchylenie ćwiartkowe.
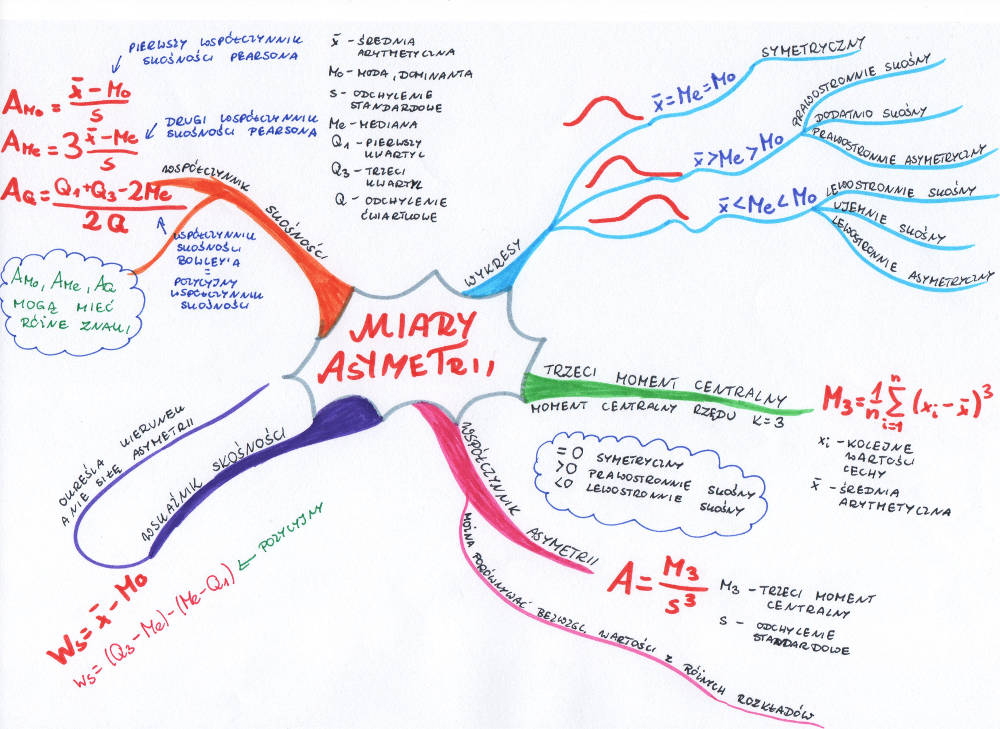
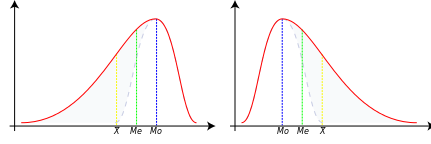
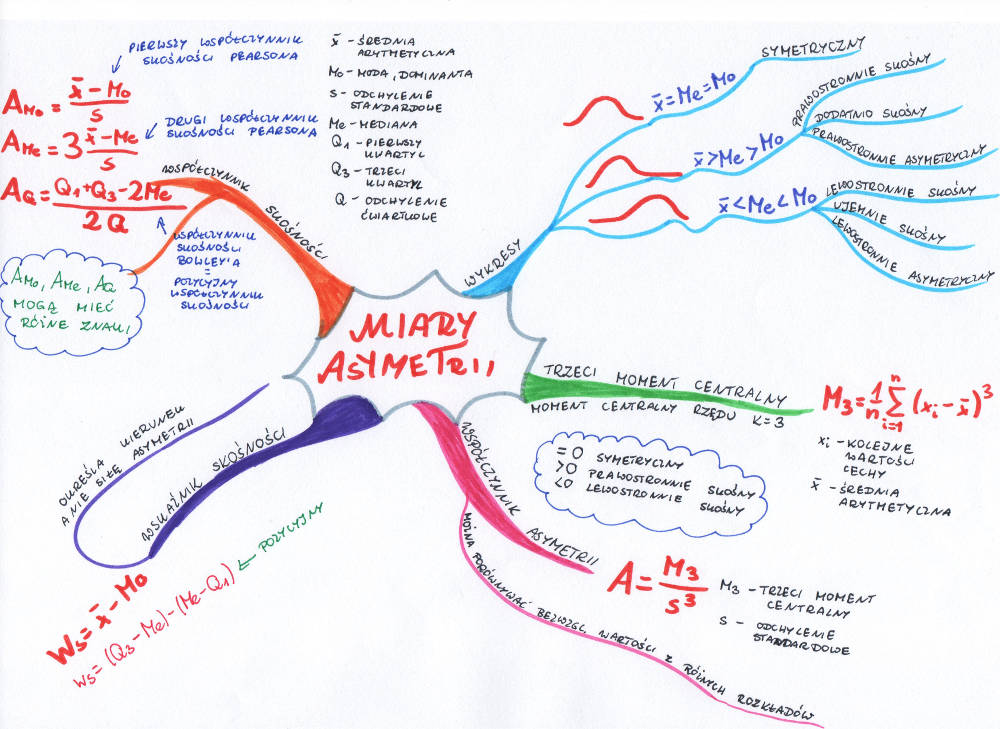
Rozkład naszej badanej cechy statystycznej może być: symetryczny, prawostronnie asymetryczny (prawostronnie skośny, dodatnio skośny) lub lewostronnie asymetryczny (lewostronnie skośny, ujemnie skośny). Rozkład symetryczny to taki, w którym średnia arytmetyczna jest równa medianie oraz modzie. Wartości mniejsze od średniej i wartości większe od średniej rozkładają się symetrycznie, wykres wygląda jak lustrzane odbicie. Rozkład prawostronnie skośny to taki, w którym średnia jest większa od mediany, która z kolei jest większa od mody. Na wykresie wygląda to tak, że z lewej strony mamy górkę, a w prawą stronę ciągnie się długie ramię. W przypadku rozkładu lewostronnie skośnego sytuacja wygląda odwrotnie. Górka znajduje się po prawej stronie, a długie ramię mamy na lewo. Średnia arytmetyczna jest tu mniejsza od mediany, a mediana jest mniejsza od mody.
Trzeci moment centralny
Pierwszym wskaźnikiem, o którym należy powiedzieć, chcąc analizować asymetrię rozkładu jest trzeci moment centralny (moment centralny rzędu k=3). Obliczamy go za pomocą wzoru:
\(M_{3}=\frac{1}{n}\sum_{i=1}^{n}(x_{i}-\overline{x})^{3}\)\(x_{i}\) symbolizuje kolejne wartości cechy, natomiast \(\overline{x}\) to średnia arytmetyczna
Jeśli wartość trzeciego momentu jest równa 0, to mamy do czynienia z rozkładem symetrycznym. Wartości większe od 0 mówią o prawostronnie asymetrycznym rozkładzie, a wartości mniejsze od 0 mówią o lewostronnie asymetrycznym rozkładzie.
Współczynnik asymetrii
Na podstawie trzeciego momentu centralnego obliczamy współczynnik asymetrii.
\(A=\frac{M_{3}}{s^{3}}\)W powyższym wzorze \(M_{3}\) to trzeci moment centralny, a \(s^{3}\) to odchylenie standardowe podniesione do trzeciej potęgi.
Współczynnik asymetrii jest o tyle lepszy od samego trzeciego momentu centralnego, że pozwala na porównywanie wartości dla różnych rozkładów. Również wartości dodatnie mówią o dodatniej asymetrii, wartości ujemne o ujemnej asymetrii, a w przypadku 0 mamy do czynienia z rozkładem symetrycznym.
Wskaźnik skośności
Kolejnym wskaźnikiem, który służy do określania asymetrii rozkładu jest wskaźnik skośności. Obliczamy go poprzez odjęcie od średniej arytmetycznej wartości mody (dominanty).
\(W_{s}=\overline{x}-Mo\)Wskaźnik skośności może być również oparty na miarach pozycyjnych (poszczególne kwartyle)
\(W_{s}=(Q_{3}-Me)-(Me-Q_{1})\)I tu również wartości dodatnie oznaczają rozkład prawostronnie skośny, a wartości ujemne rozkład lewostronnie skośny. W przypadku rozkładu symetrycznego wartość wskaźników skośności wyniesie 0.
Współczynnik skośności
Współczynniki skośności mogą być oparte na dominancie, medianie albo wyłącznie na miarach pozycyjnych. Wzory wyglądają następująco:
\(A_{Mo}=\frac{\overline{x}-Mo}{s}\)poszczególne symbole to \(\overline{x}\) – średnia arytmetyczna, Mo – moda (dominanta), s – odchylenie standardowe
Jest to tzw. pierwszy współczynnik skośności Pearsona. Mówi o tym, jaką część odchylenia standardowego stanowi różnica pomiędzy średnią arytmetyczną i dominantą.
\(A_{Me}=3\frac{\overline{x}-Me}{s}\)poszczególne symbole to \(\overline{x}\) – średnia arytmetyczna, Me – mediana, s – odchylenie standardowe
Jest to tzw. drugi współczynnik skośności Pearsona. Mówi o tym, jaką część odchylenia standardowego stanowi różnica pomiędzy średnią arytmetyczną a medianą. Wartość tę mnoży się przez 3.
\(A_{Q}=\frac{Q_{1}+Q_{3}-2Me}{2Q}\)We wzorze tym występują pierwszy i trzeci kwartyl, mediana oraz odchylenie ćwiartkowe.
Jest to miara pozycyjna. Dotyczy wyłącznie jednostek pomiędzy pierwszym i trzecim kwartylem. Określany jest również nazwą współczynnik skośności (asymetrii) Bowley’a.
Warto zwrócić uwagę, że współczynniki skośności liczone według różnych wzorów mogą przynosić różne wyniki. Potencjalne różnice mogą dotyczyć nie tylko wartości, ale również znaków.
Przykład w naszych firmach:
Myślę, że warto wrócić po przerwie również do naszego przykładu z wynagrodzeniem w czterech różnych firmach:
- „Wszystkim Równo” – zatrudnia 10 pracowników, z których każdy dostaje co miesiąc 5000 zł.
- „Szefo Górą” – zatrudnia panią sprzątaczkę, która na umowę zlecenie otrzymuje 500 zł, do tego 8 szeregowych pracowników z pensją 1500 zł i kierownika, który co miesiąc na konto przyjmuje 37500 zł.
- „Byle do Awansu” – mamy tu również 10 pracowników – pięciu pracuje poniżej roku i otrzymują 3000 zł, druga piątka ma już dłuższy staż i dzięki temu doczekała się pensji po 7000 zł.
- „Wielka Niewiadoma” – dziesięciu pracowników, każdy z inną pensją, od 1000 do 9000 zł.
W przypadku firmy „Wszystkim Równo” mamy do czynienia z sytuacją, kiedy wszyscy pracownicy otrzymują identyczne wynagrodzenie, średnia jest równa medianie i modzie. Jest to rozkład symetryczny, wszystkie miary asymetrii wynoszą 0. Pamiętajmy tutaj o zasadzie niedzielenia przez 0 i nie liczmy miar, gdzie w mianowniku (ten na dole w ułamku) jest odchylenie standardowe (współczynnik asymetrii oraz współczynniki skośności Pearsona).
Również firmy „Byle do Awansu” oraz „Wielka Niewiadoma” mają bardzo symetryczny rozkład wynagrodzeń. Nie występuje tu moda, więc nie można obliczyć miar, które się o nią opierają (wskaźnik skośności i pierwszy współczynnik skośności Pearsona). Pozostałe natomiast wynoszą 0, czyli potwierdzają nasze obserwacje o symetryczności rozkładu.
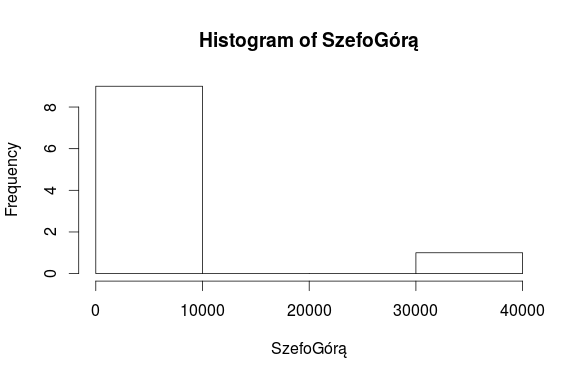
Jedynym rozkładem niesymetrycznym może się pochwalić (czy oby na pewno pochwalić?) firma „Szefo Górą”. Tutaj trzeci moment centralny to 3389400000000. Współczynnik asymetrii wynosi 2,66. Wskaźnik skośności to 3500. Pozycyjny wskaźnik skośnosci to 0. Pierwszy współczynnik skośności Pearsona to 0,32. Drugi współczynnik skośności Pearsona wynosi 0,97. Współczynnik skośności Bowley’a to 0. Zastanówmy się teraz, co oznaczają powyższe wartości. Może zacznijmy od tych różnych od 0. Trzeci moment centralny – gigantyczny. Do tego współczynnik asymetrii 2,66, co wskazuje na wysoki poziom asymetrii. Wskaźnik skośności – dodatni. Pierwszy i drugi współczynnik skośności Pearsona też zdecydowanie dodatnie. Mamy więc wyraźnie do czynienia z rozkładem prawostronnie skośnym. Mówią o tym wszystkie niepozycyjne miary asymetrii. Spodziewamy się na wykresie górki po lewej stronie i ciągnącego się ramienia w prawo. Czy tak było? Przypomnijmy sobie histogram:
Jak widać wszystkie wartości skumulowane są po lewej stronie wykresu, za wyjątkiem wynagrodzenia szefa, które wyraźnie wyróżnia się po prawej stronie wykresu.
A skąd zerowe wartości miar pozycyjnych? Przypominam, że mówią one tylko o wartościach występujących pomiędzy pierwszym i trzecim kwartylem. Pomijają wartości skrajne. A przypadku firmy „Szefo Górą” odpowiedzialnym za asymetrię jest nieproporcjonalnie wysokie wynagrodzenie szefa. I tylko szefa.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska