Regresja liniowa to temat, do którego zabieram się już od bardzo, bardzo dawna i wciąż przekładam na później. Bo nie jest szczególnie trudno opowiedzieć o wykresie kołowym. W miarę łatwo jest wytłumaczyć średnią arytmetyczną albo odchylenie standardowe. A regresja liniowa to już taki większy słoń. Ale duże słonie też się da zjeść, tylko trzeba zacząć kawałek po kawałeczku. I myślę, że właśnie tak krok po kroku uda nam się uporać z naszym regresyjnym słoniem i po przeczytaniu artykułu wszyscy już będą wiedzieć, o co chodzi.
Regresja liniowa – słów kilka tytułem wstępu
Ostatni wpis dotyczył wykresu punktowego. Pokazywałam, jak narysować zależność między dwoma zmiennymi. Wcześniej pokazywałam, jak wyliczyć, czy występuje korelacja liniowa. W regresji liniowej chodzi o coś więcej. Korelacja mówi nam, jaka jest siła zależności pomiędzy zmiennymi. Regresja mówi nam o kształcie tej zależności. Czyli do tych punkcików na wykresie spróbujemy dopasować prostą, która będzie najlepiej charakteryzować zależność między x i y. I jak już będziemy mieć taką funkcję, to wtedy można analizować powiązania między zmiennymi, a nawet prognozować y na podstawie nowo poznanego x.
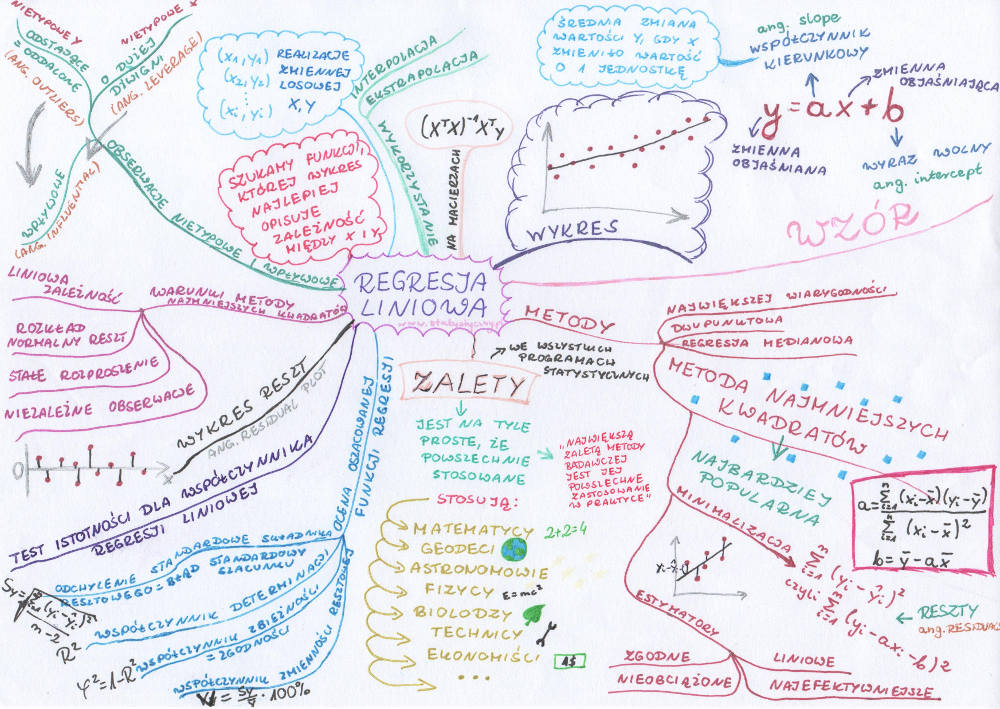
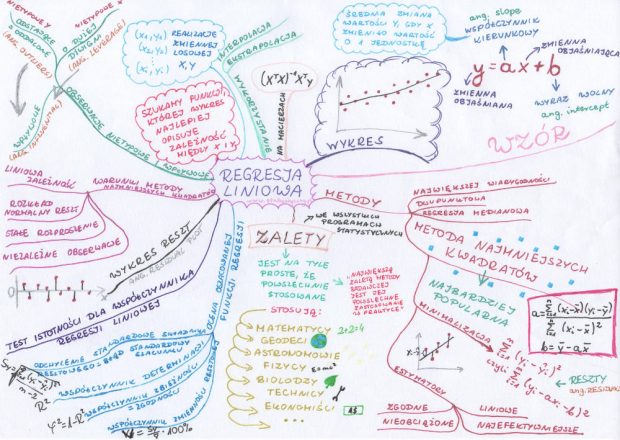
Prostą, której szukamy, opiszemy wzorem y=ax+b. Jest to najprostszy zapis. W literaturze fachowej można znaleźć dużo bardziej skomplikowanych znaczków i take opisy, że ja sama czytam po trzy razy i nie rozumiem, o co chodzi. Ale nam tu nie chodzi w tej chwili o zrozumienie całej statystyki matematycznej, która za tym stoi. Zaczniemy od tego, co w miarę łatwo pojąć.
Prosta y=ax+b zawiera cztery różne literki.
y – zmienna objaśniana (czasem nazywana też zależną)
x – zmienna objaśniająca (czasem nazywana też niezależną)
a – współczynnik kierunkowy, współczynnik regresji y względem x (ang. slope)
b – wyraz wolny (ang. intercept)
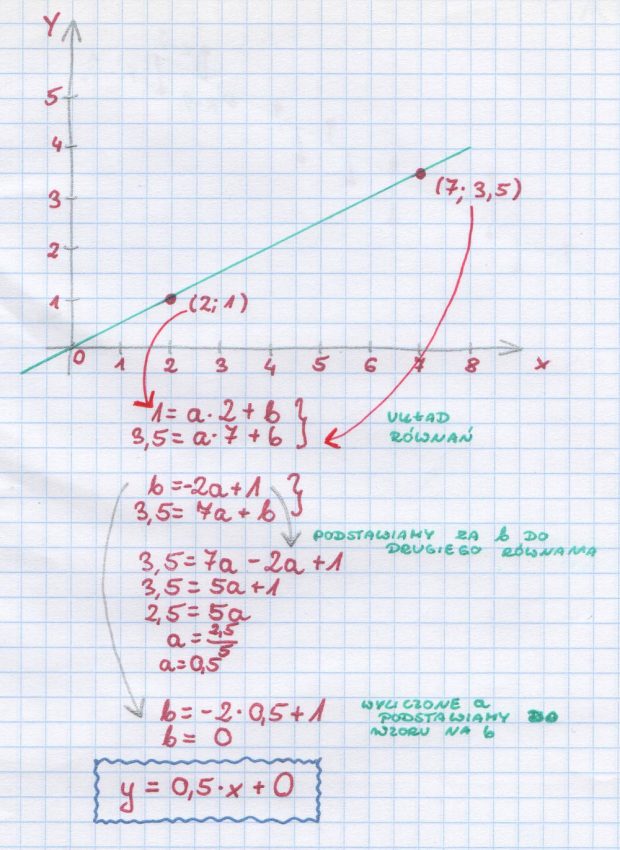
Większość z Czytelników pewnie pamięta, że w szkole należało znaleźć prostą przechodzącą przez dwa punkty. Jeśli mieliśmy takie dwa punkty, to wystarczyło rozwiązać układ równań i już mieliśmy wzór.
Klasyczna metoda najmniejszych kwadratów
W przypadku wielu punktów nie jest już tak prosto. I właściwie nigdy nie ma sytuacji, kiedy prosta byłaby w stanie przejść przez każdy z punktów. Trzeba więc wybrać taką metodę, która pozwoli znaleźć najbardziej optymalną prostą, która najlepiej przedstawi zależność pomiędzy x i y. I oczywiście metod tych jest bardzo dużo. Można usłyszeć o metodzie największej wiarygodności, metodzie dwupunktowej, regresji medianowej itp. A wśród tych wszystkich metod najpopularniejsza jest metoda najmniejszych kwadratów.
Ponieważ planujemy skupić się na tym, co najbardziej popularne, zaraz Wam napiszę, w jaki sposób do estymowania wartości a i b używa się metody najmniejszych kwadratów. Zakłada ona, że będziemy szukać minimum dla sumy kwadratów różnic wartości obserwowanych i wartości teoretycznej (obliczonej z naszego równania).
To teraz trochę wzorków. Szukamy minimum dla sumy kwadratów:
\(min\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}\)To samo możemy napisać w taki sposób:
\(min\sum_{i=1}^{n}(y_{i}-ax_{i}-b)^{2}\)Pomijając wszelkie przekształcenia, zapamiętajmy tylko, że aby obliczyć współczynnik kierunkowy korzystamy z wzoru:
\(a=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}\)Obliczenie wartości wyrazu wolnego jest już proste. Wystarczy do wzoru podstawić średnią arytmetyczną x oraz średnią arytmetyczną y.
\(b=\overline{y}-a\overline{x}\)W ten prosty sposób mamy obliczone zarówno a i b z naszego równania i możemy podać wzór regresji liniowej.
Warto zwrócić uwagę na fakt, że korzystając z metody najmniejszych kwadratów mamy do czynienia z estymatorem liniowym, zgodnym, nieobciążonym i najefektywniejszym.
Interpretacja współczynnika kierunkowego i wyrazu wolnego
Kiedy już obliczymy parametry regresji liniowej, to warto by było wiedzieć, co one oznaczają.
Jeśli chodzi o wartość współczynnika kierunkowego, to mówi on nam o tym, jaki jest wpływ jednostkowej zmiany x na zmienną y. Jeśli a ma wartość dodatnią, to wzrost x o jednostkę oznacza, że możemy się średnio spodziewać wzrostu y o a jednostek. Jeśli a ma wartość ujemną, to wraz ze wzrostem x o jednostkę, y średnio zmniejsza się o a jednostek.
Wyraz wolny mówi nam, jakiej wartości y powinniśmy się spodziewać dla zerowego x. Bardzo często nie ma on żadnego sensu – ponieważ może znajdować się poza przedziałem danych, dla których analizujemy regresję. Jeśli np. interpretujemy zależność między wzrostem a wagą, to zaczynamy nasze rozważania od pewnej niezerowej wartości x. Ktoś, kto ma 0 cm wzrostu nie może nic ważyć, nie istnieje i nie można w tym przypadku interpretować w sensowny sposób wyrazu wolnego.
Regresja liniowa – prosty przykład
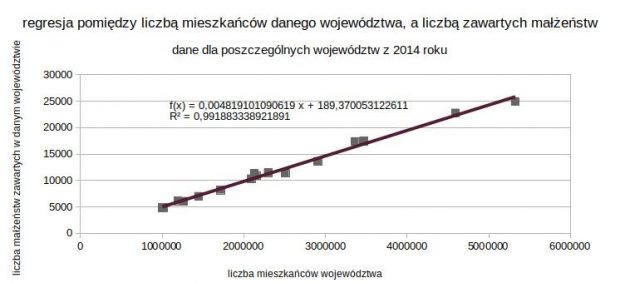
Kiedy pisałam tekst o przykładach współczynnika korelacji, to między innymi pokazywałam przykład korelacji pomiędzy liczbą mieszkańców danego województwa a liczbą zawartych małżeństw w 2014 roku. Korelacja liniowa miała bardzo wysoki współczynnik (0,9959) więc myślę, że będzie to dobry przykład do pokazania również regresji liniowej. Korzystamy z danych wyjściowych:
| województwo | x (ludność) | y (małżeństwa) |
| Dolnośląskie | 2908457,00 | 13599,00 |
| Kujawsko-pomorskie | 2090836,00 | 10294,00 |
| Lubelskie | 2151836,00 | 10911,00 |
| Lubuskie | 1020767,00 | 4875,00 |
| Łódzkie | 2508464,00 | 11405,00 |
| Małopolskie | 3364176,00 | 17361,00 |
| Mazowieckie | 5324519,00 | 24924,00 |
| Opolskie | 1002575,00 | 4822,00 |
| Podkarpackie | 2128483,00 | 11287,00 |
| Podlaskie | 1193348,00 | 6135,00 |
| Pomorskie | 2298811,00 | 11461,00 |
| Śląskie | 4593358,00 | 22765,00 |
| Świętokrzyskie | 1265415,00 | 6051,00 |
| Warmińsko-mazurskie | 1445478,00 | 6978,00 |
| Wielkopolskie | 3469464,00 | 17437,00 |
| Zachodniopomorskie | 1717970,00 | 8183,00 |
Na początku musimy sobie poobliczać wszystkie potrzebne dane do a i b
średnia arytmetyczna \(\overline{x}\) wynosi: 2405247,31
średnia arytmetyczna \(\overline{y}\) wynosi: 11780,50
| \(x-\overline{x}\) | \(y-\overline{y}\) | \((x-\overline{x})*(y-\overline{y})\) | \((x-\overline{x})^{2}\) |
| 503209,69 | 1818,50 | 915086816,72 | 253219989593,85 |
| -314411,31 | -1486,50 | 467372416,03 | 98854473427,97 |
| -253411,31 | -869,50 | 220341136,22 | 64217293302,97 |
| -1384480,31 | -6905,50 | 9560528797,97 | 1916785735700,10 |
| 103216,69 | -375,50 | -38757866,16 | 10653684578,47 |
| 958928,69 | 5580,50 | 5351301540,59 | 919544227710,47 |
| 2919271,69 | 13143,50 | 38369447424,66 | 8522147185439,10 |
| -1402672,31 | -6958,50 | 9760495286,53 | 1967489616254,10 |
| -276764,31 | -493,50 | 136583188,22 | 76598484673,60 |
| -1211899,31 | -5645,50 | 6841777568,72 | 1468699943637,97 |
| -106436,31 | -319,50 | 34006401,84 | 11328688618,60 |
| 2188110,69 | 10984,50 | 24035301846,84 | 4787828380751,72 |
| -1139832,31 | -5729,50 | 6530669234,47 | 1299217700619,10 |
| -959769,31 | -4802,50 | 4609292123,28 | 921157133216,72 |
| 1064216,69 | 5656,50 | 6019741692,84 | 1132557157953,47 |
| -687277,31 | -3597,50 | 2472480131,72 | 472350104277,22 |
| 115285667740,50 | 23922649799755,40 |
Co się wydarzyło w powyższej tabelce? Najpierw kolejno odejmujemy od x wartość średniej arytmetycznej x. Następnie to samo robimy dla y. Poszczególne różnice mnożymy (503209,69*1818,50=915086816,72). W ostatniej kolumnie mamy podniesioną do kwadratu różnicę \(x-\overline{x}\). Te wielkie pogrubione liczby na dole, to sumy poszczególnych kolumn. Właśnie te wartości podstawiamy do naszego wzoru na a:
\(a=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}\)a = 115285667740,50/23922649799755,40 = 0,004819
Następnie do wzoru na b podstawiamy obliczone wartości średnich:
\(b=\overline{y}-a\overline{x}\)b = 11780,50 – 0,004819 * 2405247,31 = 189,37
I voila. Wszystko obliczone. Oczywiście, normalnie nie robi się tego ręcznie, na kalkulatorze ani nawet wpisując sumy i różnice w arkuszu kalkulacyjnym. Zaraz Wam opiszę, jak to się robi w różnych programach, ale najpierw jeszcze odrobinka teorii.
Co to są reszty?
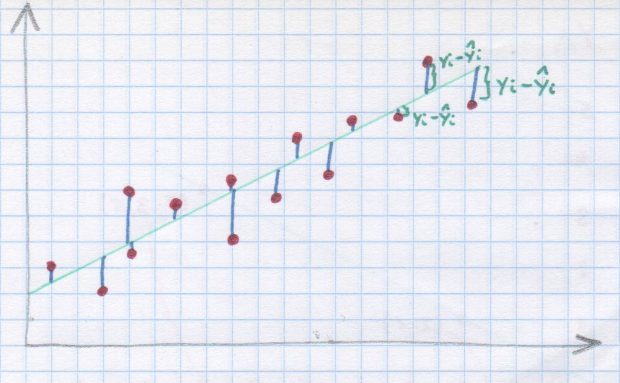
Kiedy mamy wyliczone już parametry funkcji regresji liniowej, to możemy wyliczyć, o ile nasze doświadczalne y różnią się od teoretycznego y obliczonego na podstawie funkcji regresji dla konkretnych wartości x. Każda taka różnica jest nazywana resztą albo składnikiem resztowym (po angielsku residual). To właśnie kwadraty tych różnic minimalizowaliśmy podczas obliczania parametrów a i b. I właśnie te reszty mogą nam podpowiedzieć, czy prawidłowo wybraliśmy regresję liniową jako metodę oszacowania kształtu zależności pomiędzy zmiennymi. Warto więc spojrzeć na tzw. wykres reszt. Przestawia on poziomą linię oraz kropki, które pokazują, na ile nasze reszty odchylają się od linii regresji. Reszty te powinny być dość równomiernie rozproszone z jednej i drugiej strony wykresu, najlepiej jak najbliżej poziomej linii. Jeśli dostrzegamy jakiś wyraźny układ, położenie punktów nie wygląda na losowe, to najprawdopodobniej nie mamy do czynienia z rozkładem normalnym reszt. I najprawdopodobniej regresja liniowa nie jest w takiej sytuacji najbardziej optymalną metodą szacowania y na podstawie x.
Warunki metody najmniejszych kwadratów
- Liniowa zależność – żeby regresja liniowa miała sens, to pomiędzy zmiennymi x i y musi występować zależność i zależność ta musi być liniowa
- Rozkład normalny reszt – rozkład reszt, czyli wspomnianych przed chwilą różnic pomiędzy y i y teoretycznym, powinien być albo zbliżony do normalnego albo najlepiej normalny
- Stałe rozproszenie – rozproszenie punktów dookoła obliczonej linii regresji powinno być w miarę równomierne. Czyli kropeczki z jednej i drugiej strony (i dla niskich i dla wysokich wartości x), w miarę równomiernie poodalane od tej linii.
- Niezależne obserwacje – obserwowane zmienne powinny być niezależne. Czyli w naszym przypadku liczba małżeństw w województwie wielkopolskim nie powinna zależeć od liczby małżeństw w pomorskim czy świętokrzyskim. Również liczba mieszkańców jednego województwa nie powinna zależeć od liczby mieszkańców innego.
Zalety regresji liniowej (i metody najmniejszych kwadratów)
- Przeczytałam w jakimś podręczniku, że „największą zaletą metody badawczej jest jej masowe zastosowanie w praktyce”. I właśnie to jest największą zaletą regresji liniowej (i metody najmniejszych kwadratów). Jest na tyle prosta, że stosowana jest wszędzie, gdzie tylko się da. Używają jej matematycy, geodeci, astronomowie, fizycy, biolodzy, technicy, ekonomiści i pewnie jeszcze wiele innych osób.
- Obliczenia można przeprowadzić łatwo zarówno ręcznie, jak i za pomocą przeróżnych programów statystycznych.
- Wyraźnie pokazuje, jak problematyczne są wartości odstające. Coś co jest „dwa razy dalej” od linii regresji, jest więcej niż dwa razy gorsze od punktu, który znajduje się bliżej linii regresji. Różnica ta jest istotna np. w porównaniu z metodą wykorzystującą wartość bezwzględną do oszacowania wzoru funkcji.
Obserwacje nietypowe i wpływowe
Obserwacje nietypowe dzieli się na dwie podstawowe grupy:
- Obserwacje o dużej dźwigni (ang. leverage) – mają nietypowe x i raczej typowe y. Czyli na wykresie są znacząco oddalone od pozostałych punktów na osi poziomej.
- Obserwacje odstające, oddalone (ang. outliers) – mają typowe x i nietypowe y. Czyli znacząco są oddalone od obliczonego wykresu regresji liniowej, mają dużą resztę. Mówi się o nich, że nie spełniają równania regresji.
Zarówno obserwacje odstające jak i punkty o dużej dźwigni mogą mieć wpływ na prostą regresji (zmianę współczynnika kierunkowego) lub nie. Jeśli posiadają taki wpływ, to nazywane są obserwacjami wpływowymi (ang. influential). Ich usunięcie powoduje duże zmiany w obliczonych parametrach a i b.
Przykłady obserwacji nietypowych:
- Wśród zdrowych osób o typowym wzroście i wadze pojawia się nagle ktoś chory na zespół Pradera-Williego (jednymi z objawów tej choroby jest niski wzrost i otyłość).
- Libero wśród siatkarzy.
- Badanie poziomu spalania dla różnych marek samochodów (np. w zależności od wagi) i wśród tych samochodów Tesla.
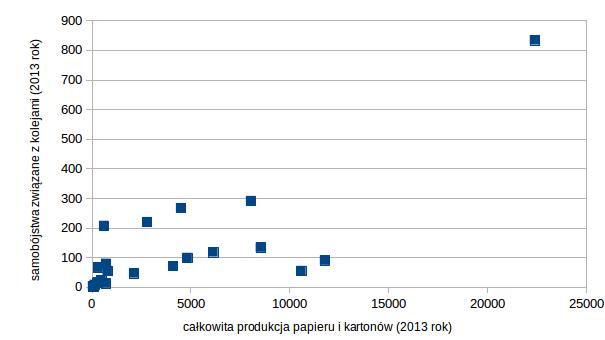
- Przykład całkowitej produkcji papieru i kartonów oraz samobójstwa związane z kolejami w 2013 roku dla poszczególnych państw europejskich. Patrzeliśmy na niego przy okazji obliczeń współczynnika korelacji, ale tutaj też się świetnie nadaje, żeby pokazać, że państwem o dużej dźwigni są Niemcy.
Ocena oszacowania funkcji regresji
odchylenie standardowe składnika resztowego
To inaczej błąd standardowy szacunku. Informuje, o ile średnio wartości empiryczne zmiennej odchylają się od wartości teoretycznych obliczonych na podstawie oszacowanej funkcji regresji. Wzorek wygląda koszmarnie, ale to tylko złudzenie, bo z gorszymi już sobie radziliśmy:
\(S_{y}=\sqrt{\frac{\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}}{n-2}}\)współczynnik determinacji
Współczynnik determinacji określa stopień, w jakim oszacowana funkcja regresji wyjaśnia zmienność zmiennej y. Przyjmuje wartości z przedziału od 0 do 1. Im bliżej 1, tym lepsze dopasowanie funkcji regresji do danych empirycznych
\(R^{2}=r_{xy}^{2}\)współczynnik zgodności (zbieżności)
Wskazuje, jaka część zmienności zmiennej y nie jest objaśniona za pomocą oszacowanej funkcji regresji. Również przyjmuje wartości od 0 do 1. W przeciwieństwie do współczynnika determinacji, im bliżej 0, tym lepsze dopasowanie funkcji regresji. Jego obliczenie jest prościutkie, bo wystarczy odjąć od 1 wartość współczynnika determinacji
\(\varphi^{2}=1-R^{2}\)współczynnik zmienności resztowej
\(V=\frac{S_{y}}{\overline{y}}*100\%\)Współczynnik zmienności resztowej informuje o tym, jaki odsetek poziomu zmiennej objaśnianej stanowią wahania losowe. Im bliżej 0, tym lepsze jest dopasowanie funkcji regresji.
test istotności dla współczynnika regresji liniowej
O testach istotności jeszcze na statystycznym nie było. Więc bez wchodzenia w szczegóły powiem tylko, że taki test jest i weryfikujemy w nim, czy współczynnik kierunkowy a jest istotnie różny od 0. Czyli sprawdzamy, czy w ogóle korzystanie z obliczonej funkcji regresji ma sens. Bo jeśli współczynnik kierunkowy jest równy zero, to znaczy, że nie ma sensu korzystanie z takiej funkcji, bo zmiana x nie wpływa na zmianę y.
Regresja liniowa w arkuszu kalkulacyjnym
W ramach wyjaśnienia. Korzystam z arkusza LibreOffice Calc. Bardzo prawdopodobne, że nie w każdym arkuszu kalkulacyjnym wszystko działa tak samo – warto w razie czego skorzystać z pomocy programu i doczytać, jakie są różnice.
Wykres
Najprościej parametry regresji (mając już gotowy wykres) można wyznaczyć poprzez kliknięcie prawym przyciskiem myszy na jeden z punktów i zaznaczenie opcji, że chcemy dodać linię trendu (w mojej anglojęzycznej wersji jest to „Insert trend line”), a następnie wybranie, że chcemy, żeby było widoczne równanie regresji (anglojęzyczna wersja „Show Equation”). Nas interesuje wykres regresji liniowej – możecie zobaczyć, że opcji różnych jest wiele.
Funkcja REGLINP (LINEST)
Inna możliwość poznania parametrów a i b (oraz wielu innych informacji), to skorzystanie z funkcji REGLINP (wersja polskojęzyczna) albo LINEST (wersja anglojęzyczna). Funkcję tę wybieramy z zestawu funkcji macierzowych (Array). Podajemy kolejno: zakres komórek dla y, zakres komórek dla x, informację czy współczynnik b ma być równy 0 (0 jeśli tak, 1 jeśli nie), informację, czy mają być policzone inne statystyki (1 jeśli tak).
Jeśli wpiszemy wszędzie jedynki to w efekcie otrzymujemy tabelkę:
| 0,004819101090619 | 189,370053122613 |
| 0,000116509255482 | 314,367367529241 |
| 0,991883338921891 | 569,855925338422 |
| 1710,84718349985 | 14 |
| 555573287,140994 | 4546300,85900633 |
Poszczególne informacje w tabelce to idąc od lewej od góry:
a = 0,0048
b = 189,37
błąd standardowy a = 0,00012 (szacunkowy błąd średni, błąd oszacowania parametru)
błąd standardowy b = 314,37
współczynnik determinacji = 0,9919
błąd standardowy y, odchylenie standardowe składnika losowego
wartość statystyki F
liczba stopni swobody dla statystyki F
regresyjna suma kwadratów
suma kwadratów reszt
Pakiet statystyczny w arkuszu kalkulacyjnym
Data -> Statistics -> Regression
Podajemy dane wejściowe i w wyniku otrzymujemy tabelę:
| Regression | |
| Regression Model | Linear |
| R^2 | 0,991883338921891 |
| Standard Error | 569,855925338427 |
| Slope | 0,004819101090619 |
| Intercept | 189,370053122613 |
W Excelu jest inaczej, niestety aktualnie nie mam dostępu więc jeśli ktoś korzysta z Excela to może sobie zainstalować pakiet Analysis ToolPack i poeksperymentować samodzielnie.
Regresja liniowa w R
Wiemy, jak wyglądają obliczenia w arkuszu kalkulacyjnym. Teraz pokażę, jak walczyć z regresją liniową w R. Przedstawiam ten sam przykład, który liczyliśmy już „ręcznie” i za pomocją funkcji w Calcu:
regresja liniowa w R – kod
dane1 <- read.csv(’~/Desktop/regresja_dane.csv’)
małżeństwa <- dane1$małżeństwa
ludność <- dane1$ludność
model1 = lm(małżeństwa ~ ludność)
plot(małżeństwa ~ ludność, main=”wykres regresji”)
abline(model1)
summary(model1)
par(mfrow=c(2,2));plot(model1);par(mfrow=c(1,1))
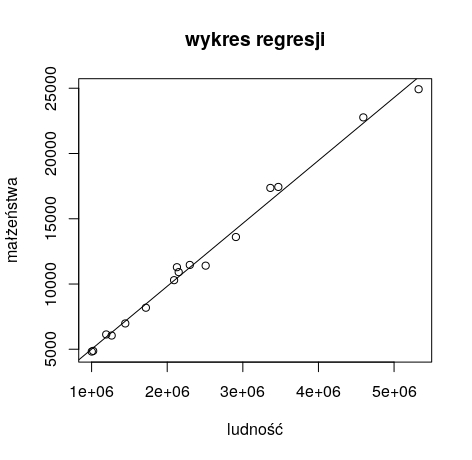
regresja liniowa w R – wykres
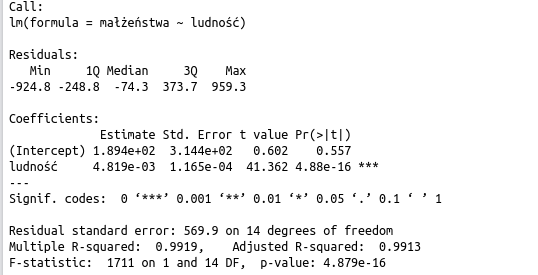
regresja liniowa w R – obliczone parametry
Jakie informacje otrzymaliśmy?
Wartości minimalne i maksymalne oraz kwartyle dla reszt.
Wartość współczynnika kierunkowego i wyrazu wolnego wraz z informacjami o odchyleniu standardowym oraz wartościami statystyki t.
Odchylenie standardowe składnika resztowego.
Współczynnik determinacji oraz skorygowany współczynnik determinacji (ten drugi bardziej przydatny w przypadku modeli z dużą liczbą zmiennych objaśniających).
Wartości dla statystyki F (która bada istotność modelu jako całości)
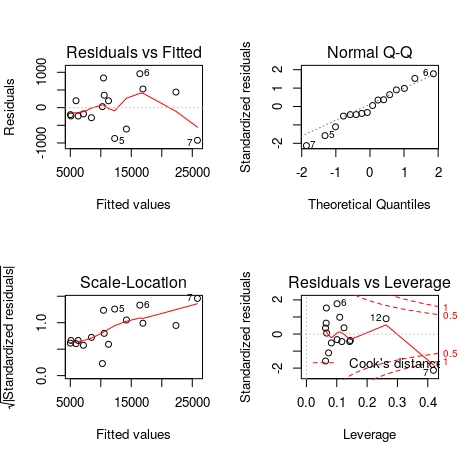
regresja liniowa w R – wykresy dotyczące reszt
Oprócz wykresu regresji liniowej, w R możemy bardzo łatwo otrzymać również cztery wykresy, które bardzo przydają się do analizy reszt.
Pierwszy wykres(“Residuals vs Fitted”) na poziomej osi ma wartości dopasowane dla zmiennej objaśnianej (y), a na osi pionowej wartości reszt. Wiadomo, najlepiej, gdyby wszystkie leżały na poziomej linii w punkcie zero (jest to idealne dopasowanie). Nas interesuje, żeby czerwona linia była jak najbardziej pozioma i prosta. Wykres ten pozwala sprawdzić, czy zależność pomiędzy x i y jest rzeczywiście liniowa.
Wykres “Normal Q-Q” to wykres kwantylowy dla rozkładu normalnego. Zależy nam na tym, by poszczególne punkty układały się jak najbliżej wykropkowanej linii. Wykres ten pozwala nam sprawdzić, czy spełniony jest warunek o normalności rozkładu reszt.
Wykres “Scale – Location” na osi poziomej przedstawia wartości dopasowane dla zmiennej objaśnianej (y), a na osi pionowej pierwiastki z modułów standaryzowanych reszt. Dobry model powinien mieć równomiernie rozmieszczone punkty wzdłuż osi poziomej. Wykres ten pozwala na sprawdzenie założenia o jednorodnej wariancji (tzw. homoskedastyczność).
Wykres “Residuals vs Leverage” pomaga wykryć obserwacje wpływowe. Mamy tu do czynienia z odległością Cooka (czyli miarą stopnia zmiany współczynników regresji, gdyby dany przypadek pominąć w obliczeniach współczynników). Interesują nas te przypadki, które wpadają poza czerwone wykreskowane linie. Im większa wartość, tym bardziej dana obserwacja wpływa na wartości współczynnika regresji.
Możemy zauważyć, że w przypadku naszych wykresów wyróżnia się siódma obserwacja. Jeśli byśmy spojrzeli do naszych danych, to możemy sprawdzić, że są to dane dla województwa mazowieckiego. Można się domyślić, że to stolica istotnie wpływa na nasze obliczenia. I należy zadać sobie pytanie, czy lepszym modelem byłby taki, który pomijałby województwo mazowieckie.
regresja liniowa – usuwanie danych z modelu
Napisałam, że można się zastanowić, czy należy usunąć ewidentnie niepasujące punkty z naszego modelu. Tak. Zawsze mamy możliwość przeprowadzenia obliczeń bez obserwacji wpływowych. Ale podejmując taką decyzję należy się bardzo starannie zastanowić, czy jest ona uzasadniona. Trzeba się zastanowić, jakie było źródło danych odbiegających od pozostałych. I podając interpretację modelu zawsze należy poinformować, że została podjęta decyzja o usunięciu z niego obserwacji nietypowych. Skoro bowiem raz miało miejsce coś „dziwnego”, to nigdy nie wiemy, czy nie powtórzy się w przyszłości. I przeprowadzając analizy na podstawie „ulepszonego” modelu, trzeba mieć świadomość, że w pewnym sensie wykluczamy przypadki nietypowe.
Interpolacja i ekstrapolacja
Kiedy poznaliśmy już wzór na naszą prostą, to możemy za jego pomocą próbować przewidywać wartości y dla znanych wartości x. Jeśli mamy klasę 1a i znamy wagę i wzrost 25 uczniów, to możemy obliczyć prostą regresji liniowej zgodnie z naszymi wcześniejszymi założeniami. I jeśli dowiadujemy się, że do klasy dołączy Tomek, który mierzy 122 cm, to możemy podstawić x do funkcji i obliczyć prawdopodobną dla niego wagę. Oczywiście, nie możemy być pewni, że Tomek będzie dokładnie tyle ważyć. Bo być może Tomek uwielbia pączki, ptysie i czekoladę i do tego 90% czasu spędza grając na tablecie w „cukierki” i w związku z tym waży 10 kilogramów więcej niż przeciętny siedmiolatek. A być może Tomek ma nogi jak patyki i mimo że rodzice karmią go chlebem ze smalcem, to i tak utuczyć ani trochę go nie mogą i boją się, że jak wiatr zawieje, to Tomek odfrunie, taki jest chudy. Nasza prognoza wagi Tomka nie będzie miała 100% pewności, ale jeśli Tomek będzie całkiem przeciętnym uczniem naszej klasy, to dzięki regresji liniowej będziemy mogli nie najgorzej przewidzieć jego wagę. I taki przypadek nazywamy interpolacją. Interesuje nas przypadek znajdujący się gdzieś wśród pozostałych punktów na wykresie.
O ekstrapolacji mówimy wtedy, kiedy chcemy prognozować y dla x spoza badanego przedziału. I tutaj trzeba uważać dużo bardziej. Bo ciężko na podstawie obliczeń przeprowadzonych dla pierwszoklasistów oszacować wagę trzyletniej siostrzyczki Tomka (o wzroście 95 cm) albo jego trzydziestoletniej mamy (która może się poszczycić wzrostem 165 cm).
Dodatkowe informacje o regresji liniowej
Pamiętajcie, że podobnie jak korelacja, regresja liniowa mówi o zależności liniowej pomiędzy dwoma zmiennymi, ale nie mówi nic o związku przyczynowo-skutkowym. Możemy próbować przewidzieć wartość jednej zmiennej na podstawie drugiej (np. wzrost na podstawie wagi), ale zmieniając jedno, niekoniecznie zmienimy wartość drugiego (jeśli odchudzimy naszego delikwenta, to nie stanie się on równocześnie niższy).
Jeśli regresja liniowa wciąż budzi wątpliwości, to polecam dwa ciekawe filmy na youtube:
Statystyka ludzkim głosem – jak obliczyć parametry regresji liniowej
Pogotowie statystyczne – o regresji liniowej w SPSS
Myślę, że po przeczytaniu powyższego artykułu oraz obejrzeniu filmów, będziecie mogli już bez problemu poradzić sobie z odpowiedzią, co to jest regresja liniowa i jak ją obliczyć.
Uffff… Artykuł ten przygotowywałam dla Was ponad miesiąc. Mam nadzieję, że było warto i że udało się wytłumaczyć dostępnie i szczegółowo regresję liniową. Wciąż mam wrażenie, że jeszcze dużo bym mogła napisać, ale chciałam, żeby artykuł już Wam towarzyszył. Jeśli uważacie, że warto przeczytać, to podzielcie się linkiem ze znajomymi. Ja tymczasem cieszę się, że pokonałam mojego słonia 😉
Niezmiennie zapraszam na fanpage statystycznego.
Na Facebooku pojawiają się zawsze informacje na temat nowych wpisów oraz przypomnienia starszych artykułów.
Przypominam również, że warto korzystać ze spisu treści, gdzie staram się na bieżąco aktualizować informacje o wszystkich artykułach na blogu.
Droga Czytelniczko! Drogi Czytelniku!
Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.
Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.
A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.
Pozdrawiam Cię serdecznie i życzę miłego dnia!
Krystyna Piątkowska