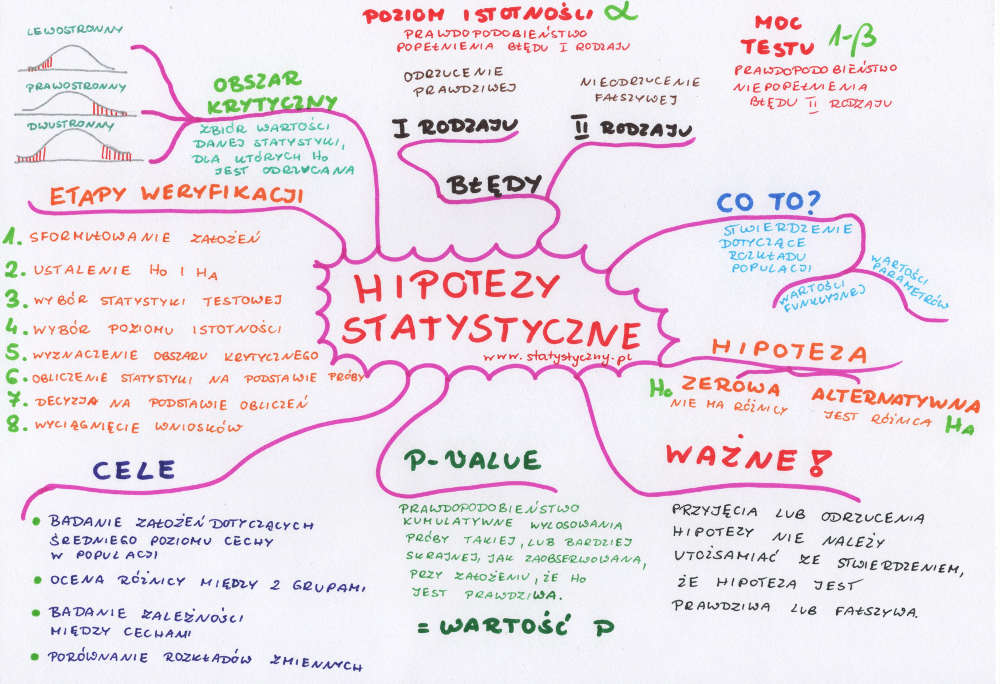
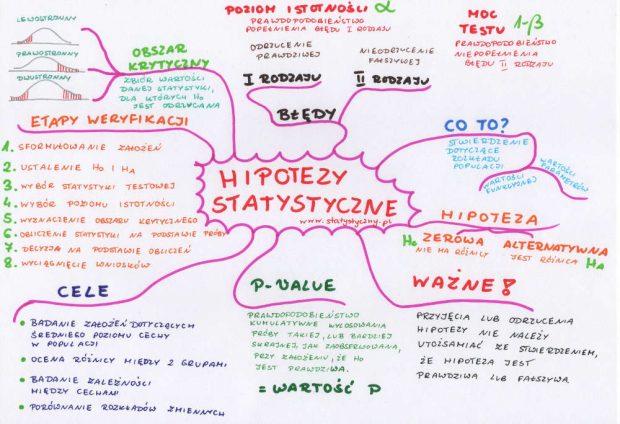
Niektórzy mówią, że hipotezy statystyczne to temat prosty i przyjemny. Nie mogę się z tym zgodzić. Pamiętam, jak bardzo mi się mieszały hipoteza zerowa z alternatywną i błąd pierwszego rodzaju z błędem drugiego rodzaju. Do tego dołączała tajemnicza wartość p-value i już w ogóle nic nie rozumiałam. Dlaczego nigdy nie przyjmujemy hipotezy zerowej, a szukamy tylko podstaw do jej odrzucenia? Czym jest moc testu i poziom istotności? Co to obszar krytyczny? Czy słysząc te pytania zaświeca Wam się w głowie czerwona lampka i macie ochotę krzyczeć RATUNKU? Jeśli tak, to naprawdę mam nadzieję, że po przeczytaniu poniższego artykułu lampka będzie zielona, a okrzyk „ratunku!” zmieni się w „ufff… hipotezy statystyczne nie są takie złe”.

Co to jest hipoteza statystyczna?

Hipoteza statystyczna to stwierdzenie dotyczące rozkładu populacji. Może dotyczyć albo jej postaci funkcyjnej (czyli jaki rozkład ma populacja statystyczna – najczęściej sprawdzanym jest rozkład normalny) albo wartości parametrów (najczęściej średniej arytmetycznej).

Hipotezy statystyczne – przykłady

Przykładów hipotez statystycznych można mnożyć oczywiście mnóstwo, a każdy może być ciekawszy od poprzedniego. Pozwolę sobie kilka tu przedstawić, żebyście wiedzieli, jakie hipotezy statytyczne możecie wymyślać samodzielnie:

• średni wzrost Polaków to 175 cm
• 30% ludzi mówi w języku angielskim
• 2% dzieci w wieku szkolnym nie lubi czekolady
• poziom szczęścia dwie minuty po zjedzeniu dużej porcji lodów jest wyższy niż przed zjedzeniem tejże dużej porcji lodów
• osoby, które uprawiają sport są zdrowsze od osób, które unikają wysiłku fizycznego
• kolejka do kasy zawsze porusza się wolniej, jeśli stoję w niej ja

Hipoteza zerowa i alternatywna

Wiemy już, czym są hipotezy statystyczne. Umiemy podać sobie różne przykłady. Warto teraz zapoznać się z pojęciem hipotezy zerowej i alternatywnej.

Hipoteza zerowa to w uproszczeniu taka, która mówi, że nie ma żadnej różnicy. Czyli (biorąc pod uwagę jeden z powyższych przykładów) możemy powiedzieć, że przed zjedzeniem dużej porcji lodów jesteśmy tak samo szczęśliwi jak po zjedzeniu tego deseru. Nie ma żadnej różnicy w poziomie naszego poczucia szczęścia, lody nie wpływają na nastrój.

Do tak postawionej hipotezy zerowej formuujemy hipotezę alternatywną. Hipoteza alternatywna mówi, że różnica jednak jest. Poziom szczęścia różni się w zależności od tego, czy dużą porcję lodów zjemy czy nie. Możemy ją sformułować na trzy różne sposoby:

1. Poziom szczęścia przed zjedzeniem lodów i po ich zjedzeniu różnią się między sobą.
2. Poziom szczęścia po zjedzeniu lodów jest wyższy niż przed ich zjedzeniem.
3. Poziom szczęścia przed zjedzeniem lodów jest wyższy niż poziom szczęścia po zjedzeniu deseru.

Po co formułować hipotezy statystyczne?

Różne mogą być cele formułowania hipotez statystycznych. Wszystko zależy od badania, jakie prowadzimy. Poniżej kilka przykładów.

• badanie założeń dotyczących średniego poziomu cechy w populacji – np. weryfikujemy dane dotyczące średniego wzrostu w populacji, badamy jaka jest średnia waga ciasteczka albo czekolady
• ocena różnicy między 2 grupami – np. sprawdzamy czy kobiety i mężczyźni są tak samo wysportowani, weryfikujemy hipotezę, że uczniowe szkół prywatnych i państwowych mają takie same oceny
• badanie zależności między cechami – np. weryfikujemy czy dobry humor zależy od ilości zjadanych lodów
• porównanie rozkładów zmiennych – najczęściej badamy czy obserwowana cecha ma rozkład normalny lub zbliżony do normalnego

Hipotezy statystyczne – błąd pierwszego rodzaju

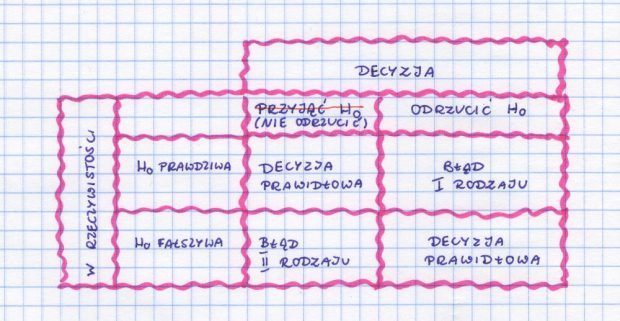
Z błędem pierwszego rodzaju mamy do czynienia wtedy, kiedy odrzucamy hipotezę zerową, a była ona prawdziwa. Jeśli więc byłoby tak, że poziom szczęścia po zjedzeniu dużej porcji lodów zupełnie się nie zmienia i właściwie jesteśmy tak samo szczęśliwi jak przed posiłkiem, a my odrzucimy tę hipotezę na rzecz hipotezy alternatywnej, że poziom szczęścia się zmniejsza (przez te okropne wyrzuty sumienia, że znowu za dużo kalorii i będzie trzeba teraz dwie godziny ćwiczyć), to popełnimy właśnie błąd pierwszego rodzaju. Bo odrzuciliśmy hipotezę zerową, która była prawdziwa.

Poziom istotności

Prawdopodobieństwo popełnienia błędu pierwszego rodzaju w sytuacji, gdy hipoteza zerowa była prawdziwa określamy symbolem α (alfa) i nazywamy poziomem istotności.

Poziom istotności określa maksymalne ryzyko popełnienia błędu pierwszego rodzaju, jakie jesteśmy skłonni zaakceptować. Wybór wartości α zależy od osoby przeprowadzającej badanie, natury problemu i od tego, jak dokładnie chcemy weryfikować swoje hipotezy. Najczęściej przyjmuje się α = 0,05. Inne popularne wartości to 0,1, 0,01 albo nawet 0,001.

Błąd drugiego rodzaju występuje wtedy, kiedy nie odrzucimy hipotezy fałszywej. Ma on miejsce w sytuacji, kiedy jednak ten poziom szczęścia przed zjedzeniem lodów i po zjedzeniu się różni. Jeśli te wyrzuty sumienia z powodu przyswojenia dużej dawki kalorii są na tyle poważne, że pomimo zjedzenia czegoś dobrego i smacznego, wcale nie czujemy się lepiej. I jeśli poziom szczęścia zdecydowanie spada nam po zjedzeniu lodów, a my stwierdzimy, że nie ma żadnej różnicy, to wtedy popełniamy błąd drugiego rodzaju. Nie odrzucamy hipotezy zerowej, mimo że jest ona fałszywa.

Prawdopodobieństwo popełnienia błędy drugiego rodzaju określamy symbolem β (beta).

Ograniczenie błędów drugiego rodzaju jest bardzo istotne w niektórych testach. Np. w przypadku medycyny lepiej powiedzieć zdrowemu pacjentowi, żeby zrobił dodatkowe badanie (kiedy w przypadku zerowej hipotezy – pacjent jest zdrowy – wyszło nam błędnie podejrzenie choroby) niż chorego pacjenta odesłać do domu bez leczenia z informacją, że jest zdrowy (błąd drugiego rodzaju).

Moc testu

Moc testu (prawdopodobieństwo, że prawidłowo odrzucimy hipotezę zerową) to 1-β. Inaczej mówiąc jest to prawdopodobieństwo niepopełnienia błędu II rodzaju.

Moc testu zależy od kilku czynników:

1. Wielkości próby użytej w badaniu (im większa próba, tym większa moc testu).
2. Rzeczywistej wielkości efektu na tle losowej zmienności w populacji.
3. Przyjętego poziomu istotności α (między błędem I i II rodzaju jest taka zależność, że jeżeli zwiększamy prawdopodobieństwo popełnienia danego błędu, jednocześnie zmniejszamy je dla drugiego).

Tabelka błędów

Test hipotezy statystycznej

Testy hipotez statytycznych to takie postępowanie, które ma na celu odrzucenie lub nieodrzucenie hipotezy. Testy dzielimy na paremetryczne oraz nieparametryczne (zgodności). Przykładami hipotez nieparametrycznych jest postać rozkładu zmiennej albo losowość próby. Wybór testu wiąże się z wyborem odpowiedniej skali pomiarowej (interwałowej, porządkowej, nominalnej – zainteresowanych odsyłam do artykułu o podziale cech wg Stevensa), jaką reprezentują analizowane dane oraz z wyborem modelu badania. Możemy mieć do czynienia z modelem zależnym albo niezależnym. Zależny to taki, kiedy pomiary są ze sobą powiązane, wykonywane sa kilkukrotnie dla tych samych obiektów. Model niezależny to taki, kiedy dokonujemy pomiarów niepowiązanych, na obiektach należących do różnych grup.

Statystyka testowa

To taka funkcja próby, na podstawie której wnioskuje się o odrzuceniu lub nie hipotezy statystycznej.

Upraszczając: na podstawie danych, które posiadamy (np. wielkości próby, jej rozkładu, rodzaju danych itp.) wybieramy, z jakich wzorów będziemy korzystać w naszych obliczeniach.

Hipotezy statystyczne – obszar krytyczny

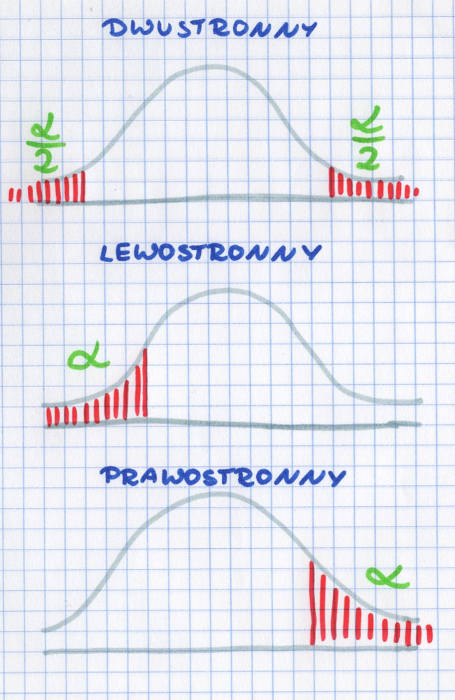
Obszar znajdujący się zawsze na krańcach rozkładu. Jeżeli obliczona przez nas wartość statystyki testowej znajdzie się w tym obszarze, to weryfikowaną przez nas hipotezę zerową odrzucamy. Wielkość obszaru krytycznego wyznacza dowolnie mały poziom istotności α, natomiast jego położenie określane jest przez hipotezę alternatywną.

Najczęściej wygląda to tak, że rysujemy sobie wykres rozkładu i zaznaczamy pod wykresem kreskami, w jakim obszarze będziemy odrzucać hipotezę zerową. Jeśli hipoteza zerowa mówi o tym, że coś jest po prostu różne, to obszar krytyczny jest dwustronny i zaznaczamy zarówno prawą jak i lewą końcówkę rozkładu. Jeśli hipoteza alternatywna jest sformułowana jako mniejsze lub większe, to zaznaczamy obszar odrzuceń albo z prawej albo z lewej strony naszego obrazka.

Winny czy niewinny

Przykład działania sądów może pomóc zrozumieć nam, kiedy przyjmujemy hipotezę alternatywną i dlaczego nieprzyjęcie hipotezy alternatywnej nie oznacza, że przyjmujemy hipotezę zerową.

Wyobraźmy sobie Pana X oskarżonego o kradzież diamentu Pani Y. Pan X staje przed sądem. Hipotezą zerową w tym przypadku jest niewinność Pana X. Zakładamy, że Pan X wcale tych diamentów nie ukradł, że zrobiła to sprzątaczka, kucharka albo Pani Y schowała je w innej szufladzie i zupełnie o tym zapomniała. Hipoteza alternatywna, to oczywiście wina Pana X. Skoro nie jest niewinny, to znaczy, że jednak ukradł diamenty i powinien zostać przez sąd skazany. Założeniem jednak podstawowym jest brak winy – sąd musi znaleźć przekonujące argumenty, żeby móc Pana X oskarżyć. Jeśli je znajdzie – to znaczy, że odrzuca hipotezę zerową (tą o niewinności) na rzecz hipotezy alternatywnej (że Pan X jest winny przestępstwa). Jeśli argumentów zabraknie, to (nawet jeśli sąd wciąż będzie podejrzewać, że coś się w zachowaniu Pana X nie zgadza i że ta niewinność wcale nie jest zbyt pewna) nie ma podstaw do odrzucenia hipotezy zerowej. To wcale nie znaczy, że Pan X nie ukradł diamentów. To tylko oznacza, że sąd nie znalazł wystarczającego dowodu.

A gdzie tu błędy? Jeśli Pan X ukradł diamenty i został skazany to sąd się nie pomylił. Jeśli diamentów nie ukradł i nie został uznany winnym, to również nie ma żadnego błędu. Jeśli nie ukradł, a poszedł do więzienia, mamy do czynienia z błędem pierwszego rodzaju. Natomiast jeśli Pan X ukradł diamenty i został uniewinniony, to mamy do czynienia z błędem drugiego rodzaju.

Hipotezy statystyczne – przykład Janiny

Być może znacie Janinę Daily, a jeśli nie znacie, to na pewno warto poznać. Janina jest bardzo miłą osobą i być może właśnie dlatego pozwoliła mi skorzystać z jej tłumaczenia, czym są hipotezy statystyczne oraz błędy pierwszego i drugiego rodzaju. Przykład jest oparty na jeżykach i rozwielitkach (i oryginalnie pojawił się gdzieś w komentarzach na Facebooku, a ponieważ takie komentarze zwykle mają krótkie życie, to mi się ich zrobiło bardzo szkoda). A komu będzie mało tego jednego janinowego przykładu, to zapraszam do wpisu: http://janinadaily.com/trudne-zycie-i-jeszcze-gorsze-metafory/. W tym wpisie możecie zapoznać się z tłumaczeniem błędu drugiego rodzaju na przykładzie owiec i farmera, a także na przykładzie testu ciążowego. Ale wróćmy do jeżyków i rozwielitek, a ja na chwilę oddaję głos Janinie…

Jeżyki i rozwielitki – opis problemu

Z błędami weryfikacji hipotez jest tak, jak z niedoborami sernika – lepiej zapobiegać, niż leczyć. Prawdopodobieństwo popełnienia błędu I rodzaju to tak zwany poziom istotności i go ustalamy sami. W większości dyscyplin wynosi 0.05, co oznacza, że akceptowalne prawdopodobieństwo, że uznamy jeżyki za mniej zabawne, mimo iż są równie zabawne co rozwielitki, a nawet sam Tadeusz Drozda, wynosi 5%. I z tym prawdopodobieństwem błędu musimy żyć. Możemy też zdecydować się na poziom istotności 0.01 i wtedy mamy tylko 1% prawdopodobieństwa, że szkalujemy jeżyki zbyt pochopnie.

Błąd II rodzaju jest związany z mocą testu, którą też możemy kontrolować, na przykład poprzez dobór odpowiedniej liczby jeżyków i rozwielitek. To, ilu zwierzątkom musimy opowiedzieć dowcipy, żeby nasze wnioski były dokładne i pewne, też można obliczyć. Ja nie policzyłam, bo trochę tu tak sobie ogólnie opowiadam, ale mogłoby się okazać, że 100 rozwielitek i 100 jeżyków, to za mała próba, i wtedy żeby mieć pewność, że nasze wnioski są słuszne, musielibyśmy iść i opowiadać dowcipy dalszym zwierzątkom.

Hipotezy statystyczne – etapy weryfikacji

1. sformułowanie założeń badania
2. ustalenie hipotezy zerowej i alternatywnej
3. wybór statystyki testowej
4. wybór poziomu istotności
5. wyznaczenie obszaru krytycznego
6. obliczenie statystyki na podstawie próby
7. decyzja na podstawie obliczeń
8. wyciągnięcie wniosków w kontekście przeprowadzanego badania

Hipotezy statystyczne – przykład weryfikacji

Żeby nie było, że cały wpis to tylko teoria, postanowiłam pokazać jeden uproszczony przykład, jak wygląda weryfikacja hipotezy statystycznej.

Wstęp

Załóżmy, że poszłam do sklepu kupić moją ulubioną 100-gramową czekoladę. Ponieważ zjadłam rano duże śniadanie, to udało się donieść czekoladę do domu. No i postanowiłam ją zważyć i z przerażeniem stwierdziłam, że moja tabliczka czekolady waży nie 100 gramów ale 95 gramów. Czy mogę z pełnym przekonaniem powiedzieć, że wszystkie tabliczki czekolady tak mają? Że jestem notorycznie oszukiwana przez producenta czekolady? Być może ta jedna czekolada to wynik błędu, a wszystkie pozostałe ważą tyle ile powinny. Być może raz dostanę czekoladę o wadze 95 gramów, a innym razem o wadze 107 gramów.

Hipoteza zerowa i alternatywna

Tak więc warto sprawdzić, jak wygląda sytuacja. Postanawiam zweryfikować hipotezę statystyczną, że kupione czekolady ważą zbyt mało.

Moja hipoteza zerowa zakłada, że producent ma rację – czekolady ważą dokładnie 100 gramów.

\(H_{0}: \overline{x}=100\)

Hipoteza alternatywna mówi o tym, że czekolady ważą mniej niż 100 gramów (będę weryfikować hipotezę lewostronną).

\(H_{A}: \overline{x}<100\)

Jako poziom istotności postanawiam przyjąć α=0,05.

Weryfikacja hipotezy

Żeby zweryfikować moją hipotezę przez 100 dni kupuję i ważę czekolady. Raz wychodzi mi mniej niż 100 gramów, innym razem więcej. Po 100 dniach wychodzi mi, że średnia waga czekolady to 98 gramów. Czy mam powód do niepokoju? Nie jest to aż tak mało jak moje 95 gramów pierwszego dnia, ale jednak mniej niż 100 gramów, które jest napisane na opakowaniu.

Na początku obliczam odchylenie standardowe – załóżmy, że wynosi 5.

Następnie liczę błąd standardowy:

\(SE=\frac{s}{\sqrt{n}}\)

W naszym przypadku błąd standardowy to ½.

Korzystam ze wzoru: \(Z=\frac{\overline{x}-μ}{SE}\)

Z = -4

Korzystając z tablicy rozkładu normalnego dla α=0,05 odczytujemy wartość -1,645. Nasza statystyka ma lewostronny obszar krytyczny (ze względu na hipotezę alternatywną, że czekolady ważą mniej niż 100 gramów). -4 jest mniejsze od -1.645 i w związku z tym odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej. Czyli odrzucamy hipotezę zerową, że czekolady ważą 100 gramów, na rzecz hipotezy alternatywnej, że ważą mniej niż 100 gramów. Nie możemy być tego w 100% pewni, ale nasze obserwacje dostarczyły nam takich dowodów, które przekonały nas do odrzucenia hipotezy zerowej z prawdopodobieństwem popełnienia błędu I rodzaju (czyli, że czekolady ważą jednak te 100 gramów) 5%.

Co to jest p-value?

P-value to prawdopodobieństwo kumulatywne wylosowania próby takiej, lub bardziej skrajnej, jak zaobserwowana, przy założeniu prawidłowości hipotezy zerowej.

Jeśli wartość p jest niższa niż przyjęty przez nas wcześniej poziom istotności statystycznej, można postępować tak jakby hipoteza zerowa została odrzucona.

O p-value możecie poczytać trochę więcej na blogu Pogotowia Statystycznego albo Statystyka w Psychologii.

Hipotezy statystyczne – podsumowanie

Hipotezy statystyczne to temat rzeka. Żeby go wyczerpać potrzeba dużo więcej niż jednego artykułu na blogu. Ale mam nadzieję, że ten jeden artykuł spowoduje, że będziecie o jeden krok bliżej do zrozumienia, o co w tym wszystkim chodzi.

---

---

Droga Czytelniczko! Drogi Czytelniku!

Dziękuję, że przeczytałaś/przeczytałeś mój artykuł. Mam nadzieję, że spełnił Twoje oczekiwania. Jeśli chcesz się podzielić swoimi przemyśleniami, to napisz do mnie na adres [email protected] albo znajdź mnie na Facebooku.

Zapraszam Cię również do zapoznania się ze spisem treści (staram się go aktualizować, choć nie zawsze to wychodzi) – jeśli lubisz statystykę, to na pewno znajdziesz coś do poczytania.

A jeśli w ramach podziękowania za ten wpis zechcesz zaprosić mnie na przysłowiową “wirtualną kawę”, to będę niezwykle zobowiązana. Co prawda kawy raczej nie pijam, ale kubek dobrej herbaty – z prawdziwą przyjemnością. A ponieważ w każdy artykuł wsadzam mnóstwo serducha i swojego wysiłku, to tym bardziej poczuję się doceniona.

Pozdrawiam Cię serdecznie i życzę miłego dnia!

Krystyna Piątkowska